Часть 2
При выполнении заданий этой части вам нужно будет записать полное решение задачи на отдельном листе. И оцениваться будет именно решение, краткий ответ здесь уже не актуален. Поэтому белое поле после текста задания — это просто кнопка для просмотра решения, рекомендуемого авторами варианта. Не спешите её нажимать, если не пытались решить задачу самостоятельно.
Первые три задания второй части относятся к алгебре.
20.
Решите уравнение
Ответ: ______
Решение. Исходное уравнение приводится к виду:
Уравнение не имеет корней. Уравнение имеет корни −5 и 1.
Ответ: −5 ; 1.
21.
Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
Ответ: ______.
Решение. Пусть искомое расстояние равно x км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно (x/4 + x/8) часа. Из условия задачи следует, что это время равно 3 часам. Составим уравнение: Решив уравнение, получим x = 8.
Ответ: 8 км.
22.
Постройте график функции
и определите, при каких значениях с прямая y = c имеет с графиком ровно одну общую точку.
Ответ: ______.
Решение. Разложим числитель дроби на множители: При x ≠ −2 и x ≠ 3 функция принимает вид:
, её график — парабола, из которой выколоты точки (−2; −4) и (3; 6). Прямая имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Вершина параболы имеет координаты (−0,5; −6,25). Поэтому c = −6,25, c = −4 или c = 6.
Ответ: c = −6,25 ; c = − 4; c = 6.
Решение типовых задач этого задания можно посмотреть на канале mathematichka на YouTube.
Задача с гиперболой и параллельными прямыми вида y = m.
Задача с параболой и пучком прямых вида y = kx.
Для индивидуальной подготовки смотрите задачи на странице «Задание на построение графиков» этого сайта. Она содержит 15 задач из банка заданий с рисунками, ответами и комментариями.
Последние три задания варианта — задания по геометрии.
23.
В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC = 6, BC = 8. Найдите медиану CK этого треугольника.
Ответ: ______.
Решение.
Ответ: 5.
24.
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.
Решение: ______.
Доказательство.Треугольники BEC и AED равны по трём сторонам. Значит, углы CBE и DAE равны. Так как их сумма
равна 180°, то углы равны 90°. Такой параллелограмм — прямоугольник.
25.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.
Ответ: ______.
Решение. Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC. Точка касания M окружностей делит AC пополам. Лучи AQ и AO — биссектрисы смежных углов, значит, угол OAQ прямой. Из прямоугольного треугольника OAQ получаем: AM2 = MQ·MO. Следовательно,Ответ: 4,5.
Примеры решения других задач, содержаших окружность, представлены в разделе Задачи по геометрии с окружностями
Переход на главную страницу сайта.
вторая часть экзамена
Вторая часть – это 6 заданий, она направлена на проверку владения материалом на повышенном уровне и делится на два модуля:
- “Алгебра”- 3 задания
- “Геометрия” – 3 задания.
Решение каждого задания этой части должно быть математически грамотным и полным.
21 задание (алгебра) – более простое
- 2 балла начисляется за правильное выполнение преобразований и полученный верный ответ.
- 1 балл начисляется если решение доведено до конца, но допущена ошибка вычислительного характера или описка с учетом которой дальнейшие шаги выполнены верно.
22 задание (алгебра) – более высокого уровня
- 2 балла начисляется за правильно составленное уравнение и полученный верный ответ
- 1 балла начисляется за правильно составленное уравнение при решении которого допущена вычислительная ошибка (решение доведено до ответа).
23 задание (алгебра) – высокий уровень сложности
- 2 балла начисляется за правильно построенный график и верный ответ на поставленный вопрос.
- 1 балл начисляется за правильно построенный график, но в ответе на поставленный вопрос возможно не все верные значения.
24 задание (геометрия) – более простое
- 2 балла начисляется за верный обоснованный ответ
- 1 балл начисляется при верных рассуждениях, но допущенной вычислительной ошибке, которая может привести к неверному ответу.
25 задание (геометрия) – более высокого уровня
- 2 балла начисляется за верное доказательство и обоснованный ответ.
- 1 балл начисляется за верное в целом доказательство, которое может содержать неточности
26 задание (геометрия) – высокий уровень сложности
- 2 балла начисляются за верный ход решения, правильные шаги и верный ответ
- 1 балл начисляется за верный ход решения, соответствующий задаче чертеж, но возможно пропущенные существенные объяснения или допущенной вычислительной ошибки.
На что обращать внимание при подготовке
Потренируйтесь решать практико-ориентированные задания (№ 1–5). Раньше этот блок назывался «Реальная математика», потом это название убрали, но задания остались теми же по смыслу. Никакой сложной математики в них нет, но нужно научиться разбираться в условии, правильно читать рисунок, понимать, что дано, а что нужно вычислить, чтобы получить ответ.
Отработайте задачи по геометрии на доказательство (№ 24). Сами по себе эти задачи несложные, но с ними часто возникают проблемы из-за неумения связно и логично излагать свои мысли, не перескакивая с одного на другое. Чтобы этому научиться, ещё раз повторите все теоремы по геометрии. Пройдитесь последовательно по ходу доказательства теоремы и поймите смысл и логику. Это поможет в решении задач на доказательство и улучшит понимание геометрии в целом.
Особое внимание геометрии
Когда в апреле провели пробный экзамен, то обнаружили много работ, в которых практически масса неудовлетворительных отметок именно по геометрии. Желательно готовить справочники по темам «Треугольники», «Четырёхугольники», «Окружность». Затем выполнить набор задач разного типа сложности по этим темам (брать задания из открытого банка)
Например, по теме «Окружность» рассматривают вопросы:
В экзаменационной работе 8 заданий по геометрии
Поскольку геометрию в школе проходят по остаточному принципу, поэтому приходится уделять ей особое внимание.
При таком подходе значительно увеличивается количество заданий, решаемых учениками и проверяемых в группе друг у друга.
прямые, отрезки и углы, связанные с окружностью;
свойства вписанных и центральных углов;
углы между хордами, касательными и секущими;
свойства хорд;
соотношения между длинами хорд, отрезков касательных и секущих;
свойства дуг и хорд, длина дуг и хорд, площадь круга и его частей;
взаимное расположение двух окружностей.. По теме «Треугольники» рассматривают вопросы:
По теме «Треугольники» рассматривают вопросы:
- признаки равенства треугольников;
- неравенство треугольника;
- определение вида треугольника;
- 4 замечательные точки треугольника;
- теорема синусов;
- теорема косинусов;
- площади треугольников;
- признаки подобия треугольников;
- вписанные и описанные треугольники.
По теме «Четырёхугольники» рассматривают вопросы:
- вписанные и описанные четырёхугольники, их свойства и площади;
- параллелограмм и его свойства;
- трапеция и её свойства;
- прямоугольник, его свойства и признаки;
- ромб, его свойства и признаки;
- квадрат, его свойства и признаки.
Задача 9 в ОГЭ по математике
Задание №9 — это квадратное уравнение, в ответ к которому надо записать единственный, больший или меньший из корней. Здесь может попасться уравнение двух типов — традиционное или дробно-рациональное.
Первый тип
Традиционное квадратное уравнение может быть двух форматов — приравненное к нулю или числу. Если первое уже готово к решению, то во втором число просто переносится к неизвестным (знак меняется на противоположный). На выходе мы получим уравнение типа: x2+ x -12 = 0.

Оно решается через дискриминант: D = b2– 4ac, где a — число рядом с квадратом, b — рядом с просто неизвестной, c — обычное число.
Здесь D = 1 – 4*1*(-12) = 49 = 72
Дальше находятся корни уравнения, то есть эти самые неизвестные. Формула: -b ± D2a. Здесь x1= -1 — 72= -4, а x2= -1 + 72= 3. Записывается в ответ требуемое число. По заданию — больший из корней.
Ответ: 3.
Второй тип
Уравнение может выглядеть как дробь. В таком случае, перед основным решением придется ввести ОДЗ — область допустимых значений, в которой уравнение под дробью нужно будет сделать неравным нулю.
Здесь ОДЗ будет таким: х+2 ≠ 0, то есть х ≠ -2 (число переносится на другую сторону, знак меняется). Если в корнях уравнения попадется число 2, мы его просто исключим.
D = 16 — 4*1*(-12) = 16 + 48 = 64 = 82
x1= 4 — 82= -2
x2= 4 + 82= 6
Ответ: 6
Что из себя представляет вторая часть ОГЭ по математике
В ОГЭ по математике вторая часть включает шесть заданий повышенной сложности (по три на алгебру и геометрию). Для их решения требуются несколько основных навыков:
- умение решать уравнения, неравенства, их системы,
- умение преобразовывать выражения,
- умение строить и читать графики, а также простые математические модели,
- умение работать с фигурами, векторами, координатами,
- умение доказывать приведенное положение,
- умение оценивать суждения на правильность или ошибочность.
Наиболее сложными заданиями являются №22 (алгебра, функции и их свойства) и №25 (геометрия, задача). Для отметки «отлично» достаточно решить правильно все остальное и один из этих номеров.
Что нужно запомнить?
- Пятое задание не страшное, многие прототипы решаются быстро и легко по единому алгоритму
- Всего существует 7 прототипов задач из модуля ОГЭ «Реальная математика». Найти все эти задания ты можешь на сайте ФИПИ
- Внимательное прочитай условие. Тогда задание станет намного проще и понятнее.
- Разбери все прототипы, тогда ты легко получишь все 5 баллов за этот блок!
Вот мы и закончили разбираться с последним заданием из блока «Реальная математика» в ОГЭ. Мы посмотрели только лишь на часть прототипов, поэтому следи за нашим блогом и жди новые статьи. Внимательно читай условие, используй алгоритм, и пусть тебе покорится пятый номер! Если захочешь разобраться с другими заданиями и эффективно подготовиться к ОГЭ по математике, напоминаем про наши онлайн-курсы.
Что нужно знать и уметь для успешной сдачи ОГЭ
- Выполнять операции с числами, десятичными и обычными дробями.
- Уметь извлекать корень, целую часть из него, оперировать свойствами корней.
- Сравнивать числа, работать с числовой осью.
- Решать уравнения: линейные, квадратные, рациональные.
- Знать и уметь применять формулы сокращённого умножения: разность квадратов, квадрат суммы и разности.
- Уметь раскладывать на множители вынесением за скобку общего множителя.
- Знать, как выглядят основные графики: линейная функция, парабола, гипербола.
- Уметь работать с алгебраическими дробями.
- Знать свойства степени.
- Знать свойства углов при параллельных прямых, что такое смежные и вертикальные углы.
- Знать основные свойства треугольника, уметь вычислять периметр, площадь, отличать биссектрису, высоту, медиану.
- Знать основные понятия окружности: вписанный и центральный угол, хорда, касательная, радиус и диаметр.
- Знать свойства основных четырёхугольников: параллелограмм, трапеция, прямоугольник, ромб, квадрат.
- Решать неравенства.
Советы по решению задач
1. Будьте уверены в себе и не торопитесь
Много ошибок в экзаменационных работах допускается из-за спешки или невнимательности.
Пример задачи
Нужно проверить все утверждения, но выбрать то, которое неверно. Очень часто ученики находят верное утверждение, отмечают его номер в ответе и спешат перейти к следующей задаче. В результате они теряют баллы на самом лёгком этапе.
Ответ: в данном случае неверно утверждение 1.
2. Внимательно читайте условие
В некоторых задачах условие формулируют так, что в нём легко запутаться
Обращайте внимание на все нюансы — если нужно, записывайте условие по пунктам.. Пример задачи
Пример задачи
Ключевые слова здесь — «в первый день каждой следующей недели». При этом цена снижается не каждый день второй недели, а только один раз, в первый день
Кроме того, важно не ошибиться с количеством дней в неделе и верно определить момент, когда цена начинает снижаться. От этого тоже зависит правильность ответа.
Ответ: 800 рублей, поскольку на восьмой день цена снизилась на 20% от 1000 рублей и была такой на протяжении всей второй недели, то есть с восьмого по четырнадцатый день. Двенадцатый день, указанный в условии, входит в этот промежуток.
3. Учите формулы
С помощью формулы решить задачу можно гораздо быстрее, чем методом сложения или подбора вариантов.
Пример задачи
Вместо того чтобы складывать значения первых шести членов прогрессии, можно найти ответ по формуле:
Знаменателем прогрессии называется отношение её соседних членов. Не путайте это понятие со знаменателем дроби.
Ответ. По условию задачи q=2. Подставляем это значение в формулу и получаем ответ: — 47,25.
Если при решении задачи с развёрнутым ответом вы используете формулу, которой нет в школьной программе, обязательно приведите и её доказательство. В противном случае вам могут не засчитать один балл.
4. Всегда выбирайте самый простой и быстрый способ решения
Особенно это касается задач с кратким ответом. Чем быстрее вы их решите, тем больше времени у вас останется на выполнение второй части работы.
Пример задачи
Здесь не нужно подставлять значения в неравенство и проверять его верность. Достаточно понять, как выглядит график функции из условия, и соотнести его с приведёнными рисунками.
x2 – 6x – 27 — это парабола f(x)=ax2+bx+c.
а>0, поэтому ветви параболы направлены вверх.
с<0, значение в нуле отрицательно, поэтому вершина параболы, в которой принимается минимальное значение, тоже лежит ниже оси Ox.
Если значение уравнения, описывающего график параболы, меньше нуля, значит, нас интересует та часть графика, которая находится ниже оси Оx. Ей соответствует некая область значений x между корнями трёхчлена, то есть — отрезок. Этому условию отвечает только рисунок 4, на нём изображён отрезок с концами в точках – 3 и 9.
Ответ: 4.
5. Решая геометрические задачи, всегда делайте рисунок
Это касается и заданий первой части, где не нужно расписывать решение. Рисунок нужен прежде всего вам, чтобы разобраться с условием задачи, всё правильно написать и найти верный ответ. Без рисунка увеличивается вероятность допустить ошибку.
Пример задачи
Рисунок для решения
6. Решайте как можно больше задач по геометрии
Геометрические задачи обычно вызывают больше затруднений, чем алгебраические. Чтобы преодолеть свой страх перед «этой ужасной геометрией» и научиться справляться с самыми разными задачами, нужно решать их как можно больше.
Какие бывают задания по реальной математике?
Для начала давайте познакомимся с заданиями №1-5 в ОГЭ по математике. Вот какие прототипы могут встретиться на экзамене:
- План домохозяйства. Этот прототип можно найти в демоверсии ОГЭ 2020, тут будет дан план домового участка или парка, с расположенными на нём объектами.
- План квартиры. Данный прототип похож на предыдущий, только работать придётся с планом квартиры и комнатами внутри этой квартиры.
- Баня и печь. В этом прототипе сюжет будет про баню, придётся делать различные вычисления для одной комнаты – парного отделения, а также подбирать печь по габаритам и стоимости.
- Лист бумаги. Вы будете работать с классическим листом формата А0, который разделён на меньшие форматы. Все вычисления придётся производить с листом бумаги.
- План местности. Будет дан план расположения различных деревень и дорог, по которым между этими деревнями можно перемещаться.
- Автомобильное колесо. На мой взгляд, это самый сложный прототип. Нужно будет работать с автомобильным колесом, которое состоит из диска и шины, а также разбираться в маркировке этих колёс.
- Телефонный тариф. Это задание полезно для учеников. Рано или поздно вы сами будете выбирать себе телефонный тариф, анализировать расход минут и гигабайтов интернета. Мне кажется, что это одно из самых интересных заданий
Задание 3
Пунктуационный анализ. Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять тире.
Полуостров Камчатка (1) омывается на западе Охотским морем, на северо-востоке (2) Беринговым, Тихим океаном (3) на юго-востоке. Камчатка на весь мир славится своими вулканами. Самый высокий её вулкан (4) Ключевская Сопка. Высота этого действующего гиганта (5) 4750 метров. Его вершина (6) самая высокая (7) точка Камчатки и Зауралья.
Правильное решение задания 3 из ОГЭ
Итак,1) Тире поставим на месте цифр 2 и 3, так как здесь пропущено сказуемое омывается, а на месте пропуска в неполном предложении ставится тире.2) На месте цифры 4 также поставим тире между подлежащим и сказуемым, выраженными именами существительными в именительном падеже.3) На месте цифры 5 тоже поставим тире между подлежащим, выраженным именем существительным, и сказуемым, выраженным именем числительным.4) На месте цифры 6 поставим тире между подлежащим и сказуемым, выраженными именами существительными в именительном падеже.5) На месте цифр 1 и 7 нет никаких знаков, т.к. нет условий для их постановки.
Правильный ответ — 23456 <или> любая другая последовательность этих цифр.
Как решать 5 задание ОГЭ по математике
Теперь мы знакомы со всеми сюжетами заданий по реальной математике. Можно приступать к разбору самого страшного задания — №5. Я хочу показать несколько заданий, и дать вам единый алгоритм. Самое интересное, что для решения этих пятых заданий даже не нужно знать само условие и то, что происходило в предыдущих четырёх пунктах.
Начнем с прототипа «План домохозяйства».
5 задание ОГЭ. Прототип «План домохозяйства»
В этом задании нам нужно посчитать самый дешёвый вариант покраски забора с внешней стороны
Почему это задание так важно? Мы интуитивно всегда стараемся найти самый дешёвый вариант, чтобы мы ни делали. Нужен ли нам для этого сам план домохозяйства? Нет! Нужно ли нам опираться на то, что мы делали в заданиях 1-4? Нет! Именно поэтому это задание не такое страшное, каким кажется сначала
Чтобы успешно выполнить данное задание, нужно внимательно прочитать всё, что нам дано. Как правило, всю таблицу нужно использовать. а если там есть что-то лишнее, то это лишнее сразу же стоит зачеркнуть, чтобы не ошибиться. В нашем случае всего 2 варианта решения и никаких лишних данных, поэтому используем всё!
Нас просят сравнить два магазина и выбрать наиболее дешёвый вариант, для этого мы просчитаем стоимость покупки необходимого количества краски отдельно в каждом магазине.
Чтобы грамотно рассчитать необходимое количество банок краски, нужно расход краски умножить на площадь забора и разделить на массу краски в одной банке, таким образом мы получим количество банок, необходимое для покраски забора. Далее нужно округлить количество банок в большую сторону, так как часть банки нам никто не продаст и целое количество банок умножить на стоимость одной банки краски, а далее к получившей сумме останется только добавить стоимость доставки заказа.
Вот так легко мы справились с заданием №5! Надеюсь, что вам уже не страшно приступать к этому номеру. Чтобы вы без проблем могли с ним справиться, поделюсь с вами алгоритмом. Он поможет ничего не упустить в ходе решения заданий.
Алгоритм решения задания №5 ОГЭ по математике
- Внимательно читаем условие. Что дано, что нужно найти?
- Зачёркиваем все лишние данные, если они есть в таблице.
- Просчитываем стоимость набора товаров или услуг отдельно для каждого магазина / сервиса.
- Сравниваем получившиеся варианты по стоимости и выбираем самый дешёвый.
- В ответ записываем то, что просят. Строго по условию!
Посмотрим еще на два задания. Чтобы вам было интереснее, мы возьмём задачи из двух самых сложных и страшных сюжетов – «План местности» и «Автомобильное колесо».
Сначала отработаем алгоритм на задаче из сюжета «План местности».
5 задание ОГЭ. Прототип «План местности»
Решение. В данном прототипе нужно посчитать, сколько денег понадобится заплатить за самый дешёвый набор продуктов
При этом не важно, какими дорогами Володя с дедушкой поедут (просёлочными или асфальтированными), не нужно знать, какой путь самый короткий. Используем наш алгоритм
Вот нам и покорился неприступный пятый номер, которым известна реальная математика в ОГЭ.
Наконец, рассмотрим пятый номер из сложного сюжета «Автомобильное колесо».
5 задание ОГЭ. Прототип «Автомобильное колесо»
Решение. Видим, что опять нас просят выбрать самый дешёвый вариант. На этот раз меняем резину на колёсах автомобиля. Алгоритм работает, меняется лишь формула подсчёта.
Задание 4
Синтаксический анализ.
Замените словосочетание «жить без забот», построенное на основе управления, синонимичным словосочетанием со связью примыкание. Напишите получившееся словосочетание.
Правильное решение задания 4 по русскому
Примыкание — способ подчинительной связи, при котором зависимое неизменяемое слово связывается с главным только по смыслу. Зависимым словом всегда выступает неизменяемая часть речи — инфинитив, наречие или деепричастие.1. Найдём главное слово: жить (без чего?) без забот; жить — главное слово.2. Зададим вопрос наречия: жить (как?) беззаботно => (в неиз-мен. ч. речи).
Следовательно, правильный ответ — житьбеззаботно <или> беззаботножить.
Применение групповой работы на уроках математики при подготовке к ОГЭ.
Психологи давно доказали, что люди лучше всего усваивают то, что обсуждают с другими, а лучше всего помнят то, что объясняют другим.
Учащиеся под руководством учителя создают группы по 3- 4 человека.
Алгоритм действий учащихся.
Задания обязательного уровня (1 часть)
Выполнив задания 1 части, сравнивают решения с ответами и между собой.
Делают работу над ошибками.
Получают другой вариант заданий 1 части и выполняют только те задания, в которых были допущены ошибки. Каждая группа получает задание и готовится самостоятельно. При этом учащиеся не знают, кто будет выполнять задание у доски.
Задания 2 части
Представители каждой группы решают задания по порядку, возможно, только те, которые решить смогли.
Остальные учащиеся проверяют задания, задают вопросы, оценивают. Оценку получает вся группа. Каждая группа готовится самостоятельно в течение недели. Проверку осуществляют на элективе.
Задания повышенной сложности
Задания у доски выполняют те учащиеся, которые с ним справились самостоятельно.
Остальные при этом имеют возможность разобраться в затруднениях, встретившихся при выполнении этих заданий.
Если есть несколько учащихся, решивших задание, то проверку можно осуществлять в виде математического боя.
Задачи для тренировки и самопроверки.
Задача 1
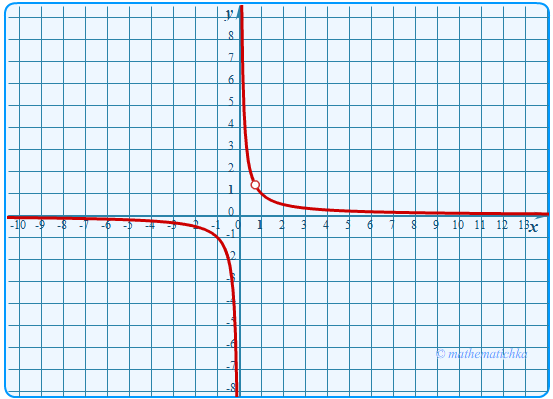
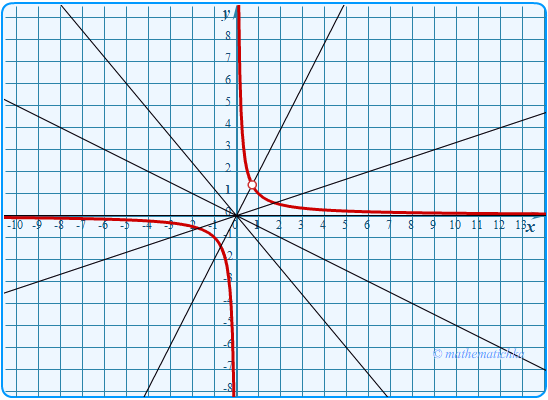
Постройте график функции
\
Определите, при каких значениях \(k\) прямая \(y=kx\) имеет с графиком ровно одну общую точку.
Показать ответ
Ответ: k = 1,96
Задача 2
Постройте график функции \ Определите, при каких значениях \(m\) прямая \(y=m\) имеет с графиком ровно две общие точки.
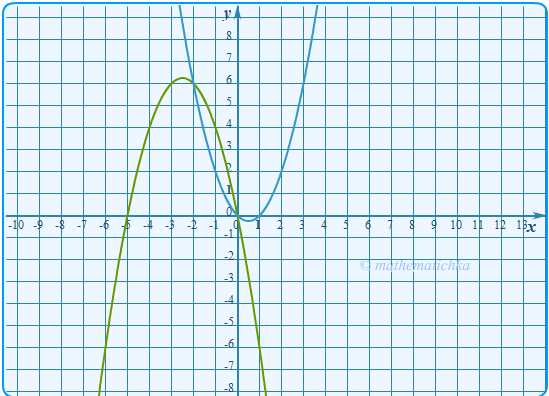
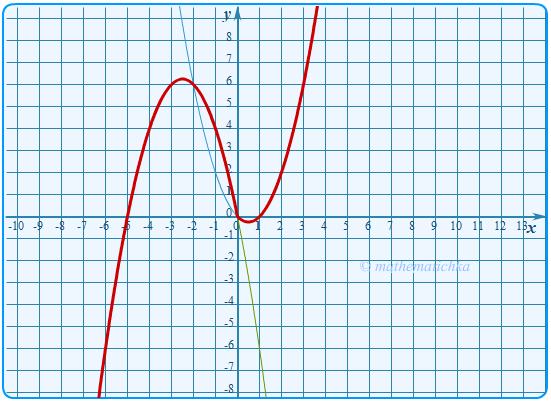
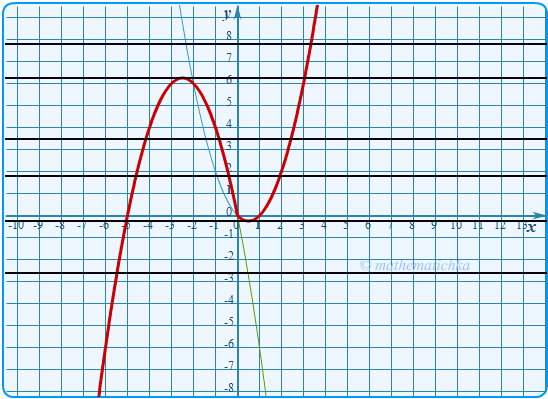
Показать ответ
Ответ: m = −0,25 и m = 6,25
Задача 3
Постройте график функции \ Определите, при каких значениях \(m\) прямая \(y=m\) имеет с графиком ровно две общие точки.

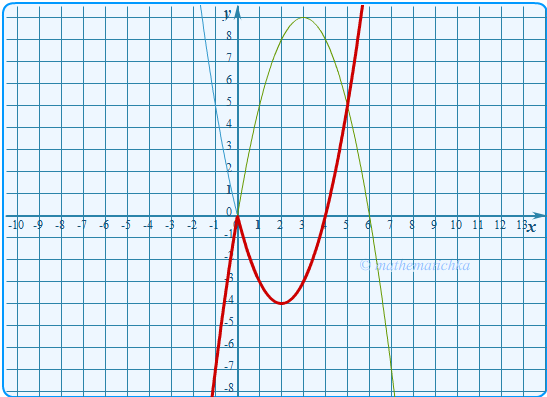
Показать ответ
Ответ: m = −4 и m = 0
Задача 4
Постройте график функции \ Определите, при каких значениях \(m\) прямая \(y=m\) имеет с графиком ровно три общие точки.
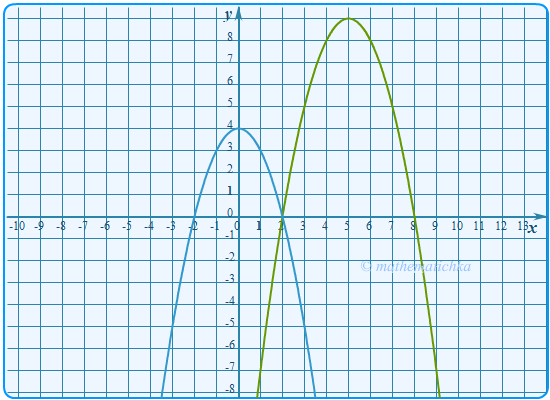
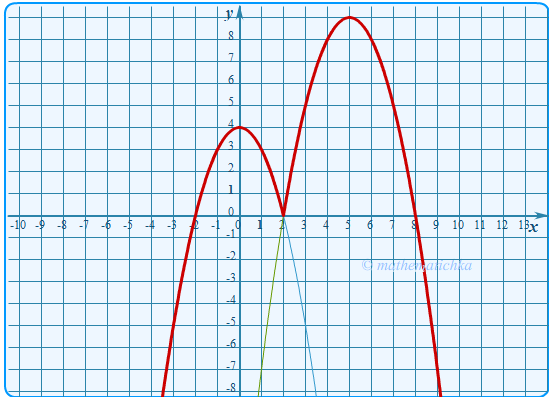
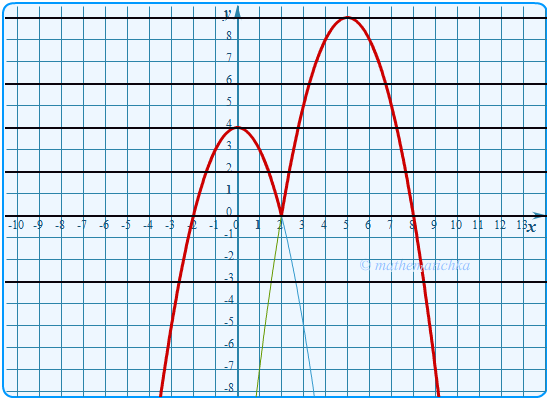
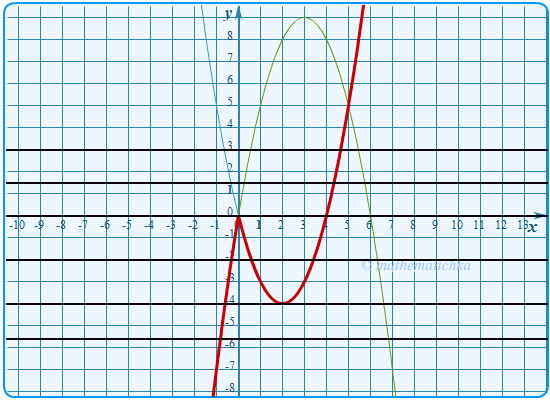
Показать ответ
Ответ: m = 0 и m = 4
Задача 5
Постройте график функции \ Определите, при каких значениях \(m\) прямая \(y=m\) имеет с графиком ровно три общие точки.
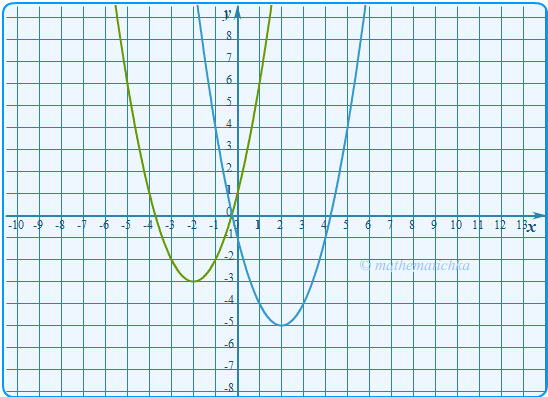
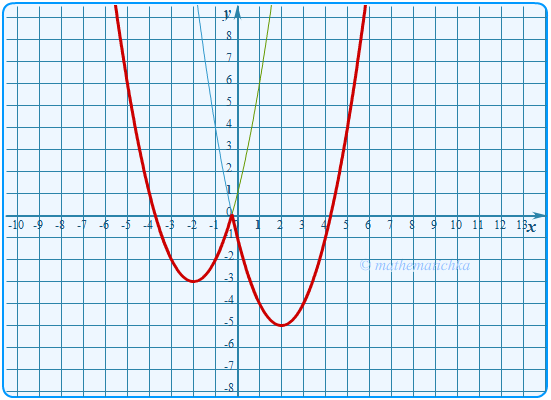
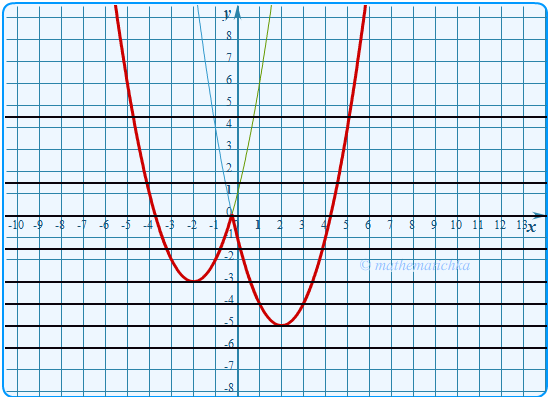
Показать ответ
Ответ: m = −3 и m = 0,0625
Задача 6
Постройте график функции \ Определите, при каких значениях \(m\) прямая \(y=m\) имеет с графиком ровно одну общую точку.
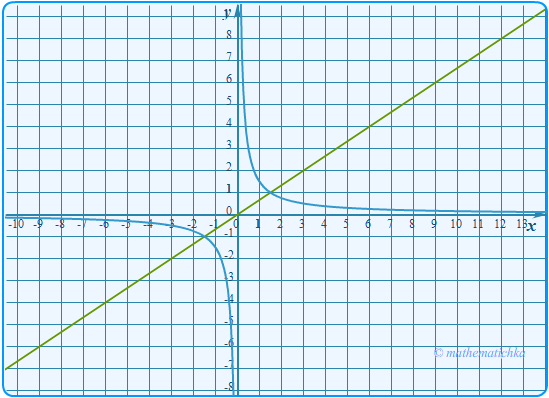
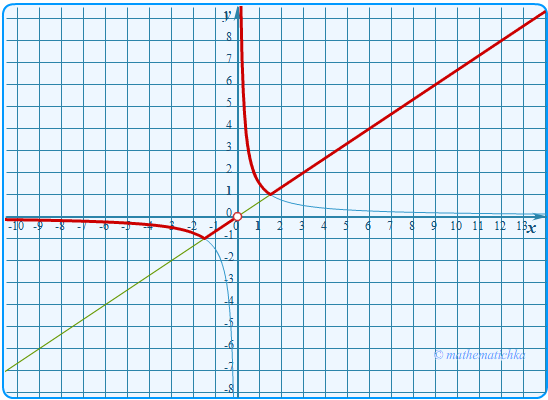
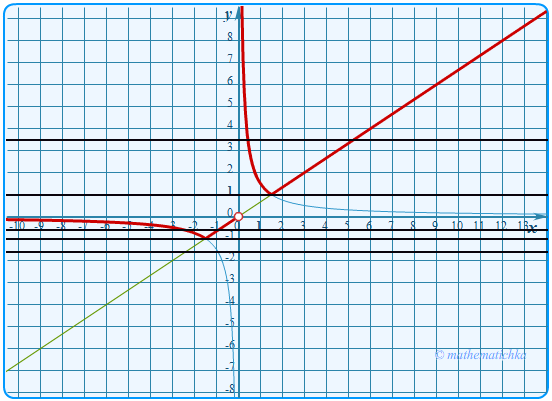
Показать ответ
Ответ: m = −1 и m = 1
Задача 7
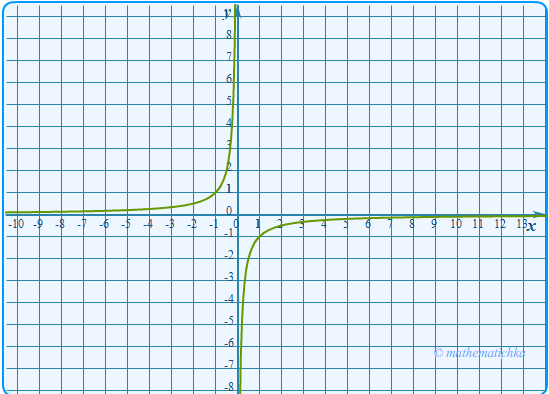
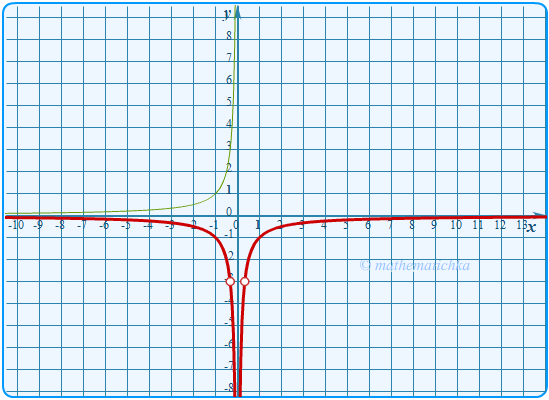
Постройте график функции \ Определите, при каких значениях \(k\) прямая \(y=kx\) не имеет с графиком общих точек.
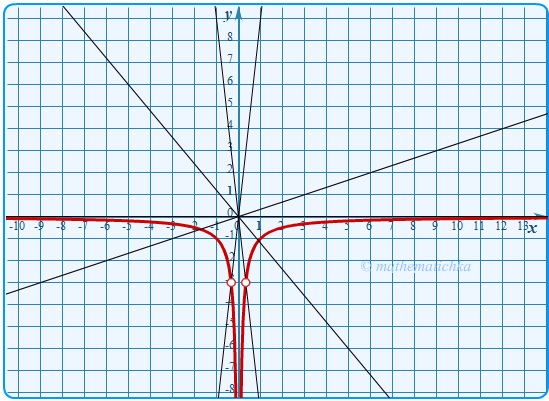
Показать ответ
Ответ: k = ±9 и k = 0
Задача 8
Постройте график функции \
и определите, при каких значениях \(m\) прямая \(y=m\) имеет с графиком одну или две общие точки.
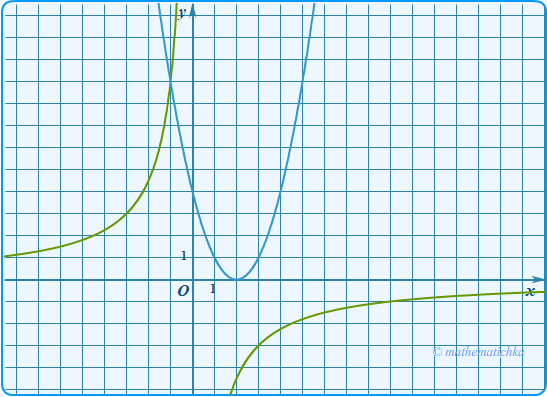
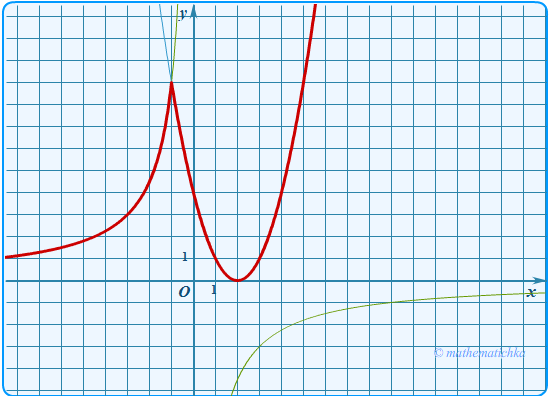
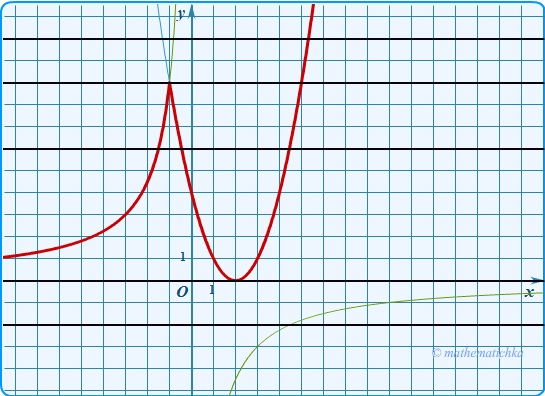
Показать ответ
Ответ: m = 0 и m = 9
Задача 9
Постройте график функции \ Определите, при каких значениях \(m\) прямая \(y=m\) имеет с графиком ровно две общие точки.
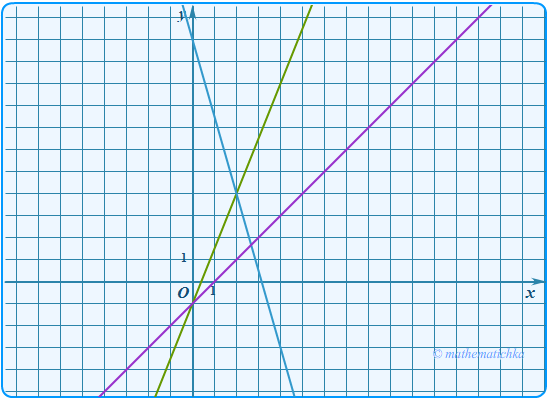
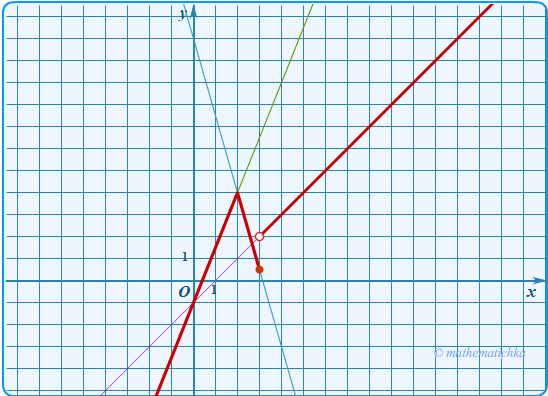
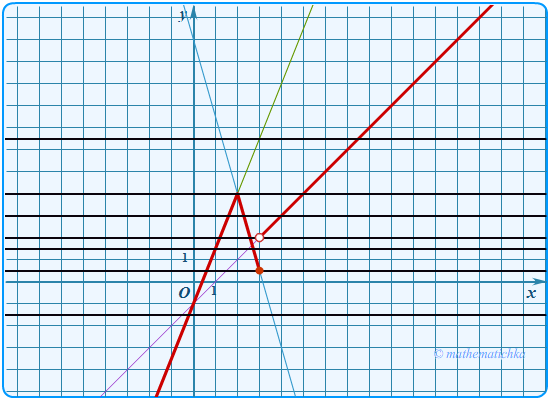
Показать ответ
Ответ: m ∈ ∪{4}
Задача 10
Постройте график функции \ Определите, при каких значениях \(k\) прямая \(y=kx\) имеет с графиком ровно одну общую точку.
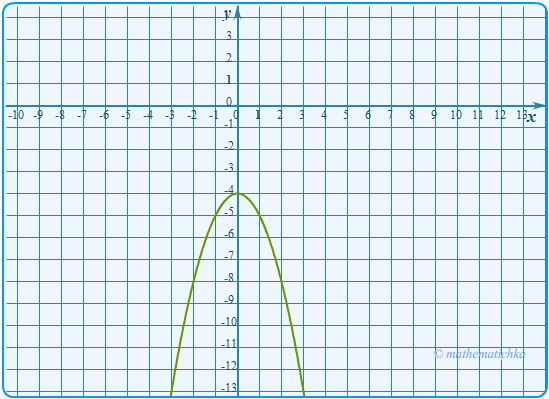
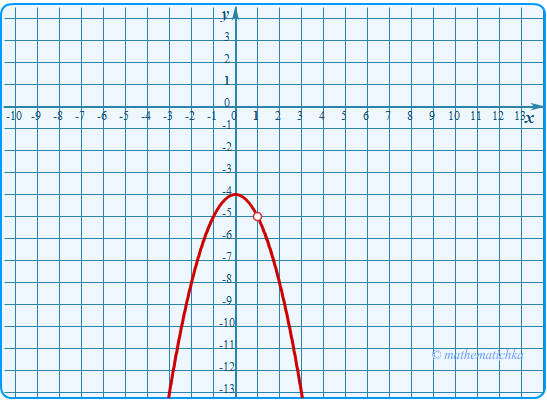
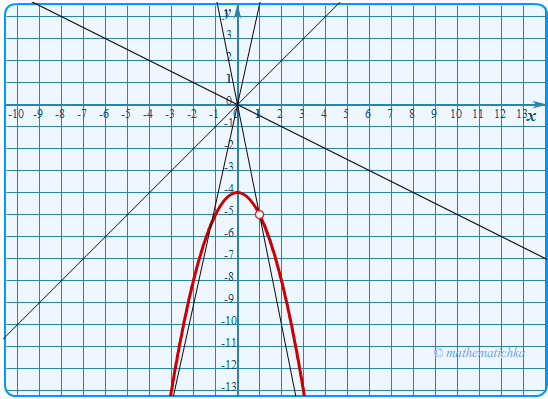
Показать ответ
Ответ: k = −5
Задача 11
Постройте график функции \[y =\left\{ \begin{array}{ccc} -x^2-2x+3 \\-x-1 \hspace{16pt}\end{array} \begin{array}{ccc}\text{при}\;\; x\ge -2,\\ \text{при}\;\; x
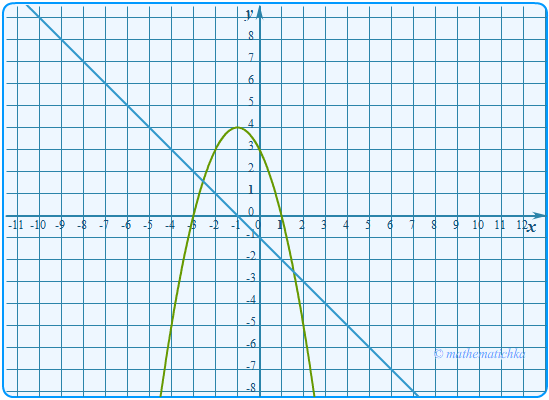
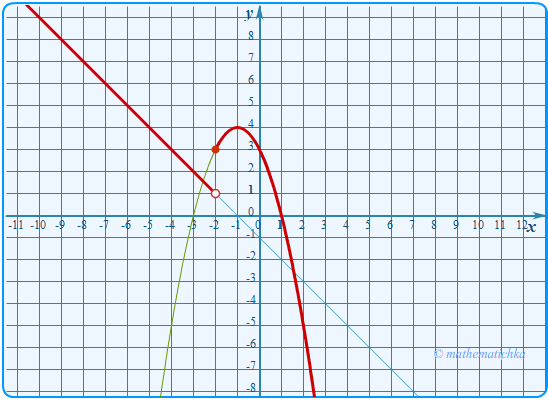
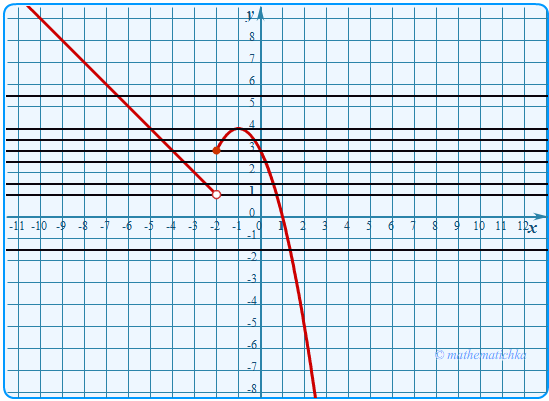
Показать ответ
Ответ: m ∈ (1;3)∪{4}
Задача 12
Постройте график функции \ Определите, при каких значениях \(m\) прямая \(y=m\) не имеет с графиком
ни одной общей точки.
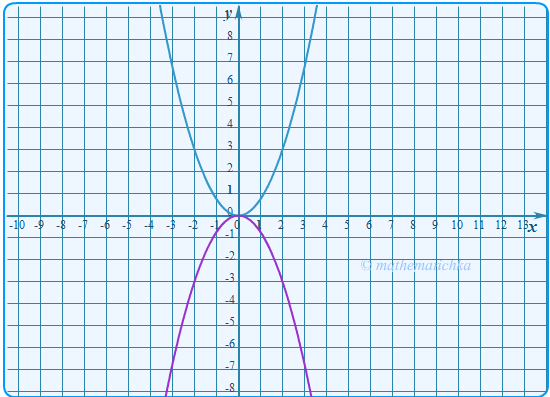
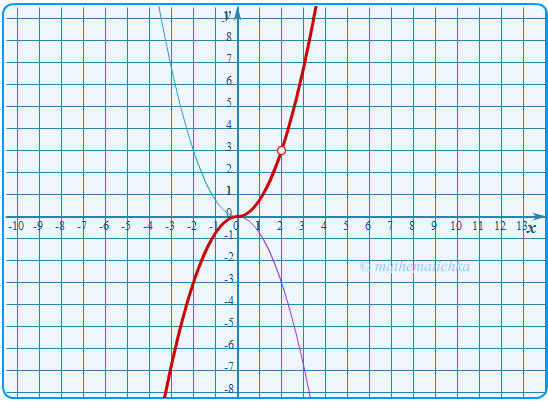
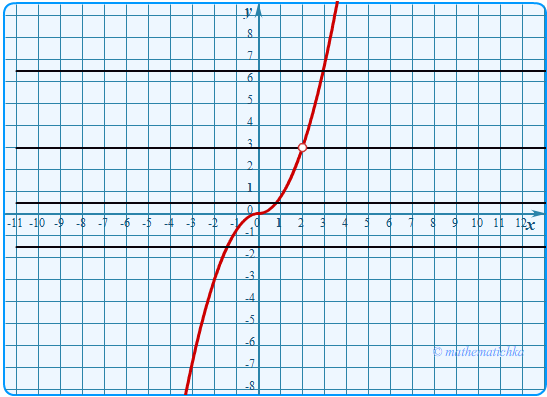
Показать ответ
Ответ: m = 3
Задача 13
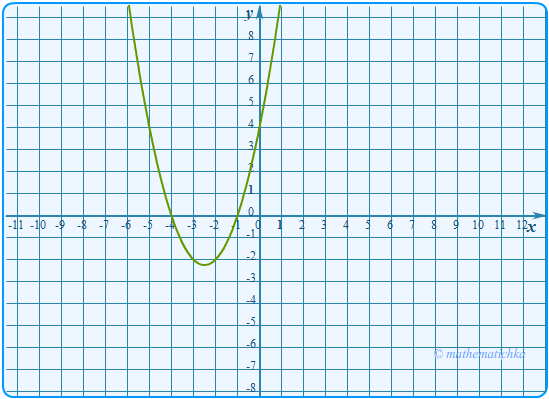
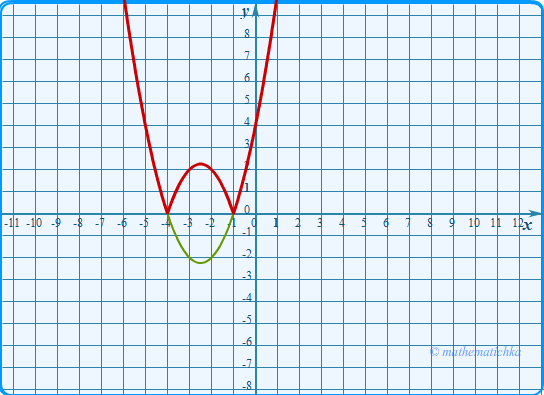
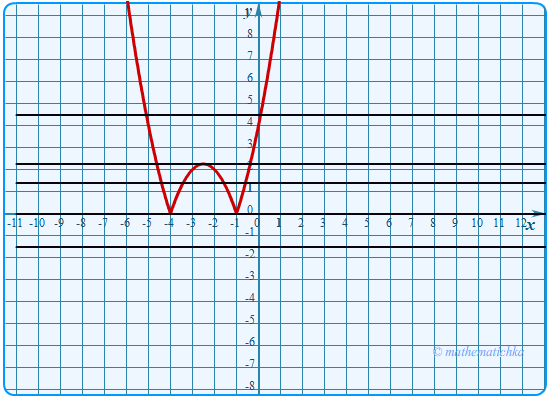
Постройте график функции \ Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Показать ответ
Ответ: 4
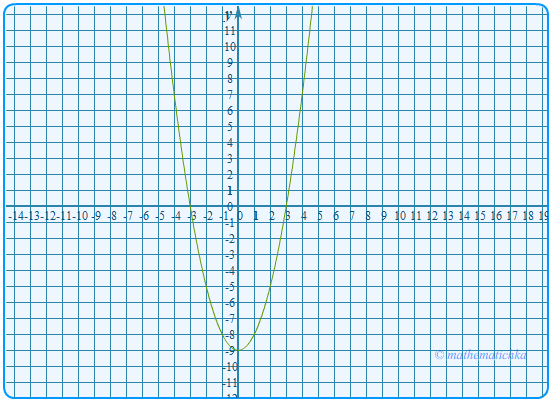
Задача 14
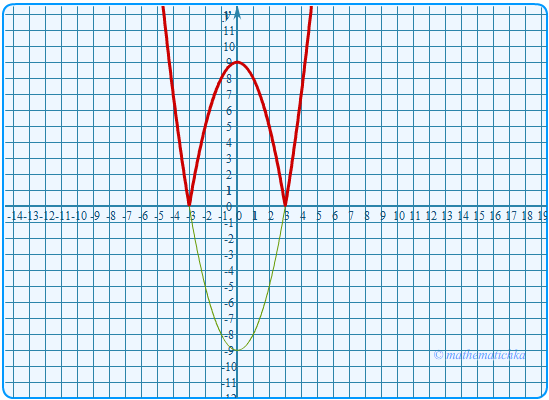
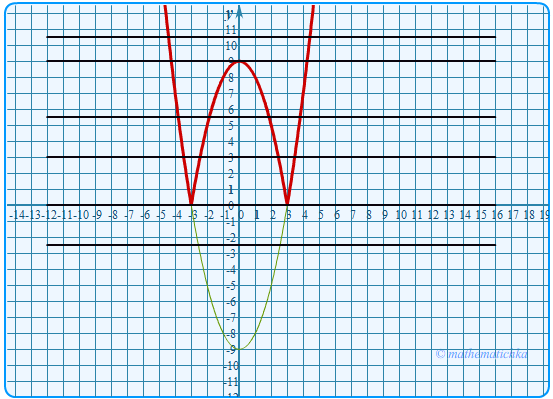
Постройте график функции \ Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Показать ответ
Ответ: 4
Задача 15
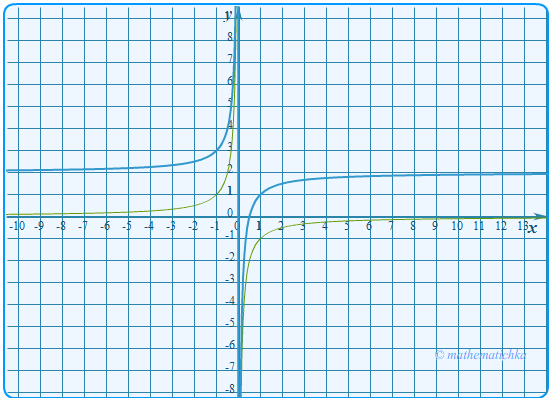
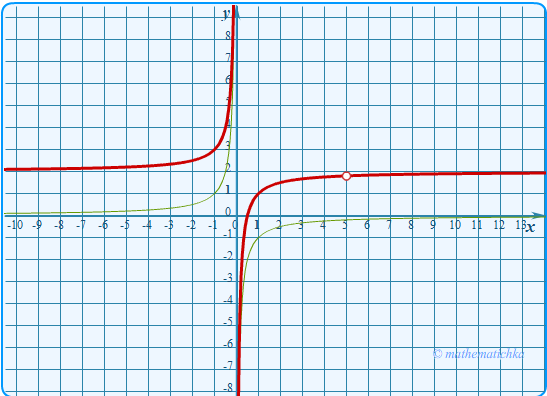
Постройте график функции
\
Определите, при каких значениях \(m\) прямая \(y=m\) не имеет с графиком общих точек.
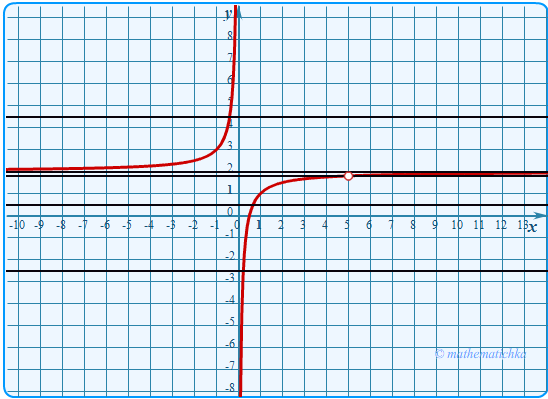
Показать ответ
Ответ: m = 1,8 и m = 2




