Бесплатно
ЕГЭ.рф
Сайт: https://егэ.рф
Платформа бесплатного тестирования уровня подготовки школьников к ЕГЭ по математике базового и профильного уровней — на основе реальных заданий от ФИПИ 2021.
Первая часть экзамена будет проверена сразу после сдачи и ты увидишь свои результаты незамедлительно. Также ты сможешь получить детальный разбор ошибок в письменных заданиях от экспертов ЕГЭ.
А по итогу ты сможешь сопоставить свои результаты с проходными баллами в ВУЗы и выбрать, куда поступать.
«4ЕГЭ»
Сайт: https://4ege.ru
Каждый видеоурок состоит из двух основных частей: простое изложение самой важной и необходимой теории по заданной теме и решения основных задач ЕГЭ
«Синергия»
Сайт: https://synergy.ru
Для вашего удобства на сайте собрано все, что может потребоваться для подготовки к экзамену по математике:
- Демоверсии и КИМы, ЕГЭ предыдущих периодов
- Теория и практика по каждому типу задания
- Официальная информация и новости
Весь теоретический материал по математике разделен на вопросы из ЕГЭ и собран в файлы. Просто выбирайте интересующую тему (вопрос, раздел), открывайте лист и повторяйте (или учите, если забыли).
Информация изложена кратко, но просто и понятно. Схематическая подача поможет все быстро запомнить.
В практическом разделе собраны готовые решения самых сложных тестов. Просто выбирайте задание и смотрите подробный план решений задач того или иного типа.
Для удобства разбора листы разделены на 2 части. В первой — только сами задачи, которые можно решать самостоятельно. Во второй части — те же задачи, но с расписанным решением.
«РешуЕГЭ»
Сайт: https://mathb-ege.sdamgia.ru
Здесь регулярно выкладывают тренировочные варианты ЕГЭ по математике базового и профильного уровней. Каждый месяц — новый вариант. По окончании тестирования система проверит ваши ответы, покажет правильные решения и выставит оценку.
Чтобы тренироваться по определённым темам, вы можете составить свой вариант — по конкретным разделам задачного каталога.
Также на сайт размещен курс из 100 занятий «Д. Д. Гущин. Готовимся к ЕГЭ по профильной математике«. В нем рассмотрены все экзаменационные темы, дано большое количество заданий из школьной математики, материалов ЕГЭ, математических олимпиад и вузовских вступительных испытаний.
Занятия включают в себя конспекты, видеоуроки с разбором простых и сложных случаев, упражнения для мгновенной самопроверки и варианты для самостоятельной работы.
Для начала нужно авторизоваться на сайте и пройти входное тестирование, чтобы был построен ваш индивидуальный образовательный маршрут.
«Математика ЕГЭ 100БАЛЛОВ»
Сайт: https://vk.com
Страница для самоподготовки к ЕГЭ по математике волонтерского некоммерческого проекта. Ежедневно размещаются различные задания и полезные материалы для подготовки к экзамену по математике.
Есть теория в картинках, видеоуроки по отдельным темам, практические задания и пробные варианты ЕГЭ.
«Математикс»
Сайт: https://www.youtube.com
Канал создан в помощь тем, кто готовится к ЕГЭ по математике.
Здесь вы найдете плейлисты, посвященные следующим темам:
- Уравнениям и Неравенствам №13 и №15 ЕГЭ
- Задачам ЕГЭ №17 №18 №19
- Стереометрии и Планиметрии №14 и №16 ЕГЭ
- Высшей Математике (Теория с примерами)
- Разборам задач из вариантов Ларина
- Разборам вариантов СтатГрад
«ЕГЭ и ОГЭ на 80-ballov. Годограф»
Сайт: https://www.youtube.com
На ютуб-канале выложены короткие видеоуроки по основным темам подготовки «ЕГЭ по Математике 2021 80 баллов». Всего в плейлисте 261 видео. Для бесплатного просмотра открыто примерно 20% полного курса.
Полный курс, включающий в себя не только видеоматериал, доступен по платной подписке на сайте проекта 80-ballov.ru. Можно сначала оценить качество материала и подачи и, при необходимости, оплатить полный доступ.
Канал Бориса Трушина
Сайт: https://www.youtube.com
Личный канал преподавателя математики онлайн-школы «Фоксфорд».
Здесь вы найдете короткие и ёмкие видеоуроки по следующим темам:
- Задания 1-12. ЕГЭ. Математика. Профильный уровень
- Задания 13-19. ЕГЭ. Математика. Профильный уровень
- Разборы вариантов ЕГЭ
- Подборки по темам: Квадратный трёхчлен, Планиметрия, Неравенства, Теория вероятностей, Тригонометрия, Теория чисел и др.
Лайфак, чтобы решать задания на производную в ЕГЭ
Давайте посмотрим на некоторые задания, которые можно решить гораздо быстрее, не прибегая к использованию алгоритмов. Лайфхаки не работают на абсолютно всех заданиях, поэтому будьте аккуратны, применяя их!
Лайфхак, которые мы рассмотрим сегодня, будет опираться на знание формата экзамена. № 11 – задание из части с кратким ответом, ответ на который мы пишем в клеточки на бланке, а чего в этих клеточках не может быть? Очевидно, что бесконечную дробь, буквы ?, ln(…), log(…), ?, sin?, бесконечность и прочие знаки мы не сможем записать, и это очень сильно упрощает нам задачу.
Разбираем лайфхак на примере
Чтобы выполнить данное задание, необходимо знать таблицу производных и немного порассуждать логически. Если мы пойдём по алгоритму, нам придётся брать производную от e в степени (x-9), а производная от данной функции будет равна тому же самому. И получается, что мы никак не можем избавиться от символа, которого просто не может быть в ответе.
Или можем? Есть замечательная степень, которая абсолютно любое основание может превратить в единицу — это 0. Таким образом, мы можем избавиться от е, если представим её степень (х – 9) равной нулю. Получается х – 9 = 0, тогда х = 9.
Но единственный ли это способ избавиться от «е»? На самом деле нет, так как есть ещё один множитель – скобка. Ее можно занулить, тогда занулится и всё произведение. Получим 10 – х = 0, тогда х = 10. Но не стоит забывать, что найти нас просят наименьшее значение ФУНЦИИ, поэтому теперь подставим найденные х в исходную функцию.
При х = 9 получаем 1, а при х = 10 получаем 0. Видим, что значение 0 меньше, чем 1, а значит именно его мы запишем в ответ
Обратите внимание, что оно достигается при х = 10, поэтому критично важно учитывать как степень экспоненты, так и множитель-скобку
В этой статье мы рассмотрели два алгоритма, с помощью которых можно решить абсолютно любое задание № 11 ЕГЭ по математике. А еще вы узнали лайфхак, как можно выполнить задание на производную в ЕГЭ, не прибегая к использованию алгоритма, и сэкономить время!
- Учите производную
- Пользуйтесь алгоритмами
- Не забывайте про крутые лайфхаки, но будьте внимательны, применяя их!
Если хочешь разобраться в остальных темах по математике и не только, почитай другие статьи в блоге и обрати внимание на наши онлайн-курсы. Уже более 150 тысяч выпускников подготовились с нами к ЕГЭ
Кстати, у меня на курсах MAXIMUM тоже можно поучиться!
Производная и первообразные функции
В задании №7 профильного уровня ЕГЭ по математике необходимо продемонстрировать знания функции производной и первообразной. В большинстве случаев достаточно просто определения понятий и понимания значений производной.
Первый вариант задания (демонстрационный вариант 2018)
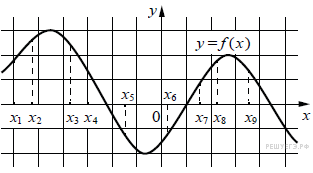
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1, x2, …, x9. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.
Алгоритм решения:
- Рассматриваем график функции.
- Ищем точки, в которых функция убывает.
- Подсчитываем их количество.
- Записываем ответ.
Решение:
1. На графике функция периодически возрастает, периодически убывает.
2. В тех интелвалах, где функция убывает, производная имеет отрицательные значения.
3. В этих интервалах лежат точки x3, x4, x5, x9. Таких точек 4.
Ответ: 4.
Второй вариант задания (из Ященко, №4)
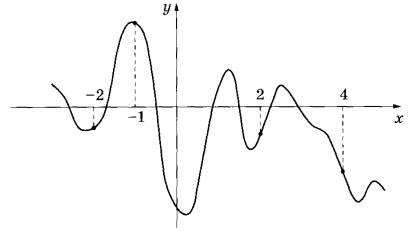
На рисунке изображён график функции у = f(x). На оси абсцисс отмечены точки -2, -1, 2, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Алгоритм решения:
- Рассматриваем график функции.
- Рассматриваем поведение функции в каждой из точек и знак производной в них.
- Находим точки в наибольшим значением производной.
- Записываем ответ.
Решение:
1. Функция имеет несколько промежутков убывания и возрастания.
2. Там, где функция убывает. Производная имеет знак минус. Такие точки есть среди указанных. Но на графике есть точки, в которых функция возрастает. В них производная положительная. Это точки с абсциссами -2 и 2.
3. Рассмотрим график в точках с х=-2 и х=2. В точке х=2 функция круче уходит вверх, значит касательная в этой точке имеет больший угловой коэффициент. Следовательно, в точке с абсциссой 2. Производная имеет наибольшее значение.
Ответ: 2.
Алгоритм решения:
- Приравняем уравнения касательной и функции.
- Упрощаем полученное равенство.
- Находим дискриминант.
- Определяем параметр а, при котором решение единственное.
- Записываем ответ.
Решение:
1. Координаты точки касания удовлетворяют обоим уравнениям: касательной и функции. Поэтому мы можем приравнять уравнения. Получим:
2. Упрощаем равенство, перенеся все слагаемые в одну сторону:
3. В точке касания должно быть одно решение, поэтому дискриминант полученного уравнения должен равняться нулю. Таково условие единственности корня квадратного уравнения.
4. Получаем:
Ответ: 4.
InternetUrok

Курсы подготовки к ЕГЭ по математике двух направлений:
Базовая математика
- Количество занятий: 49
- Длительность курса: ~200 часов
- Видеоконсультации с репетитором: 1 раз в неделю (на тарифе «Репетитор онлайн»)
Основная цель — научить пониманию математики и применению этого понимания на практике, а не просто решать задачи из банка заданий и ЕГЭ прошлых лет.
Подробно рассмотрим темы, которые входят в программу ЕГЭ базового уровня, восполним пробелы в знаниях
Обратите внимание, что в курсе нет тем и заданий, которые не предусмотрены в базовом уровне ЕГЭ по математике
Профильная математика
- Количество занятий: 60
- Длительность курса: ~240 часов
- Видеоконсультации с репетитором: 1 раз в неделю (на тарифе «Репетитор онлайн»)
Цель курса – вооружить вас знаниями, помочь сформировать навыки и отработать их на практике, что в конечном итоге позволит успешно сдать ЕГЭ.
Вы можете начать заниматься независимо от текущего уровня подготовки. Занятия можно проходить в любое удобное время и в комфортном темпе. Чтобы вы не сомневались в том, что успешно усвоили тему, каждое занятие оценивается в баллах.
Для тренировки и закрепления полученных знаний и навыков есть специальные тренажеры, в которых использованы задачи ЕГЭ прошлых лет.
Задания с развернутым ответом: немного статистики
Многие думают, что эта часть ЕГЭ по математике очень сложная. Поэтому ребята, которые не рассчитывают на высокие баллы, даже не приступают к ней. И очень зря! С помощью этих заданий можно заработать дополнительные баллы и побороться за высокое место в рейтинге.
Сейчас будет немного статистики. В среднем около 30% учеников получают полные 2 балла за решение № 12, а вот неравенство № 14 дается хуже, только около 12% с ним справляются на полный балл. Геометрия даётся ещё хуже: стереометрию № 13 полностью решают 2% выпускников, планиметрию (№ 16) менее 5%. А вот с экономической задачей (№ 15) справляются около 15%, а это целых 2 балла! Что касается № 17 и 18, то они даются ещё хуже, но на то они и самые сложные, хотя 1 балл за № 18 по статистике получают около 25% сдающих — там нужно просто привести пример.
Какие темы важно знать для ЕГЭ по математике 2022?
В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.
Формулы тригонометрии
Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул
Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.
Квадратные уравнения
Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 8 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.
Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.
Треугольники
Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии. и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем
Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще
Проценты
Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 8 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.
Дорогие выпускники, уважаемые учителя и родители!
Невозможно переоценить роль математики и математического образования в жизни современного общества
Важность математического образования и роль, которую оно играет в жизни страны, отмечены в Указе Президента Российской
Федерации от 07.05.2012 и в Концепции развития математического образования, принятой Российским Правительством в декабре 2013 года
Экзамен по математике является обязательным для всех выпускников российских школ. Это свидетельство и признание того, что
математические знания нужны каждому гражданину.
Экзамен по математике является вступительным требованием на ряд специальностей высших и средних специальных учебных заведений.
Абитуриенты, планирующие поступать на эти специальности, должны сдавать профильный экзамен.
Необходимый для поступления балл определяется требованиями приемной комиссии вузов и ссузов.
В то же время Концепция развития математического образования направлена на переход от единых образовательных программ к разнонаправленному обучению,
учитывающему образовательные запросы как школьника и его семьи, так и общества в целом.
В этой связи с 2015 года ЕГЭ по математике проводится на двух уровнях требований: базовом и профильном.
Базовый экзамен предназначен для тех, кто планирует поступать на специальности, где экзамен по математике не является вступительным требованием.
Профильный экзамен предназначен для тех, кто планирует продолжать свое математическое образование, для тех, кому важно признание
высокого уровня математической подготовки.
Вы находитесь на сайте открытых банков математических задач. Банк заданий базового уровня содержит все задания, которые могут быть включены в экзамен
Банк профильного уровня содержит задания с кратким ответом профильного ЕГЭ по математике, хотя значительная часть заданий может
использоваться при подготовке и к базовому экзамену. Разработка новых экзаменационных задач ведется постоянно и при появлении
новых заданий в ЕГЭ прототипы и аналоги этих заданий заблаговременно публикуются на нашем сайте.
Мы обновили не только внешний вид, но и функционал сайта: появилась онлайн-подготовка к ЕГЭ базового уровня.
Администрация проекта «Открытый банк» совместно с разработчиками задач продолжает работать над улучшением сайта.
Документы, регламентирующие содержание и уровень сложности задания – демонстрационные варианты, спецификации – опубликованы на
сайте федерального института педагогических измерений (ФИПИ) fipi.ru и в разделе
«Документы» на нашем сайте.
Нужно хорошо понимать, что спецификации и демонстрационные варианты отражают структуру экзамена и уровень требований к выпускникам,
но не охватывают весь спектр возможных заданий.
Мы всегда рады получать и стараемся учитывать замечания и предложения по формулировкам и составу заданий Открытого банка, по
функционалу работы сайта. Все отзывы и предложения, замечания и сообщения о неполадках, пожалуйста, присылайте на адреса электронной
почты info@mathege.ru или support@mathege.ru.
Теория к заданию 7 из ЕГЭ по математике (профильной)
Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:
$f'(x_0)={lim}{△x→0}{△f(x_0)}/{△x}$
Дифференцированием называют операцию нахождения производной.
Таблица производных некоторых элементарных функций
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n$ | $nx^{n-1}$ |
| ${1}/{x}$ | $-{1}/{x^2}$ |
| $√x$ | ${1}/{2√x}$ |
| $e^x$ | $e^x$ |
| $lnx$ | ${1}/{x}$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | ${1}/{cos^2x}$ |
| $ctgx$ | $-{1}/{sin^2x}$ |
Основные правила дифференцирования
1. Производная суммы (разности) равна сумме (разности) производных
$(f(x) ± g(x))’= f'(x)±g'(x)$
Найти производную функции $f(x)=3x^5-cosx+{1}/{x}$
Производная суммы (разности) равна сумме (разности) производных.
$f'(x) = (3x^5 )’-(cos x)’ + ({1}/{x})’ = 15x^4 + sinx — {1}/{x^2}$
2. Производная произведения
$(f(x) · g(x))’= f'(x) · g(x)+ f(x) · g(x)’$
Найти производную $f(x)=4x·cosx$
$f'(x)=(4x)’·cosx+4x·(cosx)’=4·cosx-4x·sinx$
3. Производная частного
$({f(x)}/{g(x)})’={f'(x)·g(x)-f(x)·g(x)’}/{g^2(x)}$
Найти производную $f(x)={5x^5}/{e^x}$
$f'(x)={(5x^5)’·e^x-5x^5·(e^x)’}/{(e^x)^2}={25x^4·e^x-5x^5·e^x}/{(e^x)^2}$
4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))’=f'(g(x))·g'(x)$
$f(x)= cos(5x)$
$f'(x)=cos'(5x)·(5x)’=-sin(5x)·5= -5sin(5x)$
Физический смысл производной
Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.
$v(t) = x'(t)$
Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?
Решение:
1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции
$v(t) = x'(t) = 1,5·2t -3 = 3t -3$
2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:
$3t-3 = 12$
$3t = 15$
$t = 5$
Ответ: $5$
Геометрический смысл производной
Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.
$k = tgα$
Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:
$f'(x_0) = k$
Следовательно, можем составить общее равенство:
$f'(x_0) = k = tgα$
На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.
На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.
На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.
На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение:
Касательная к графику возрастает, следовательно, $f'(x_0) = tg α > 0$
Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.
Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)
$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$
$f'(x_0) = tg ВАС = 0,25$
Ответ: $0,25$
Производная так же применяется для нахождения промежутков возрастания и убывания функции:
Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.
Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.
На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.
В ответ запишите количество данных точек.
Решение:
Отрицательным значениям производной соответствуют интервалы, на которых функция $f (x)$ убывает. Поэтому, выделим на рисунке интервалы, на которых функция убывает.
В выделенных интервалах находятся точки $х_2, х_4$. В ответ напишем их количество $2$.
Ответ: $2$
Поиск наибольшего / наименьшего значения функции
Перейдём ко второму прототипу, в котором нужно найти наибольшее/наименьшее значение функции. Интересно, что второй прототип можно отличить даже визуально, потому что кроме самой функции вам будет дан ещё промежуток, ограничивающий функцию в двух точках . Так как мы про эти точки ничего не знаем, их придётся дополнительно учитывать. В остальном начало этого алгоритма будет совпадать с предыдущим. Начинать всегда будем именно с точек экстремума, потом проверим, как ведёт себя функция в каждой точке экстремума, а также в начале и конце заданного промежутка, и в итоге запишем в ответ нужное значение функции.

Задачи для практики
Задача 1
Найдите значение выражения $\log_5 27 ⋅ \log_3 25$.
Решение
$ log_5 3^3· log_3 5^2 = 3 log_5 3 · 2 log_3 5 $
Воспользуемся свойством: $log _b (a)= 1/{log _a (b)}$
$6 · log_5 3 · {1}/{log_5 3} = 6$.
Ответ: 6
Показать решение
Полный курс
Задача 2
Найдите значение выражения $ {14} / {\sin^2 25°+ \cos^2 205°}$.
Решение
Учитывая, что $cos(180° + 25) = — cos 25$,
$cos^2 (180° + 25) = (- cos 25°)⋅(- cos 25°)=cos^2 25°$
получим ${14}/{sin^2 25° + cos^2 (180° + 25°)} = {14}/{sin^2 25° + cos^2 25°} = 14$.
Ответ: 14
Показать решение
Полный курс
Задача 3
Найдите значение выражения $ {5} / {\cos^2 33°+ \cos^2 123°}$.
Решение
Учитывая, что $cos(90°+α)=-sinα$, получим:
$cos^2 (123°)=cos^2 (90°+33°)=(-sin 33°)⋅(-sin 33°)=sin^2 33°$, таким образом
$ {5} / {\cos^2 33°+ \cos^2 (90°+33°)}= {5} / {\cos^2 33°+ \sin^2 33°}= 5$.
Ответ: 5
Показать решение
Полный курс
Задача 4
Найдите значение выражения ${18(\sin^2 16°- \cos^2 16°)} / {\cos 32°}$.
Решение
Применив формулу двойного аргумента $cos 2α = cos^2 α — sin^2 α$, получим
$cos 32°=cos^2 16° — sin^2 16°$
${18(sin^2 16° — cos^2 16°)}/{cos^2 16° — sin^2 16°} = {18(sin^2 16° — cos^2 16°)}/{-( sin^2 16°-cos^2 16° )}=-18$.
Ответ: -18
Показать решение
Полный курс
Задача 5
Найдите значение выражения $(1-\log_3 18)(1-\log_6 18)$.
Решение
$(log__3 3 — log_3 18)(log_6 6 — log_6 18) = log_3 {1}/{6} · log_6 {1}/{3} = log_3 6^(-1) · log_6 3^(-1) = log_3 6 · log_6 3 = log_3 6 · 1/(log_3 6) = 1$.
Ответ: 1
Показать решение
Полный курс
Задача 6
Найдите значение выражения $ {\log_{3} 36} / {2+\log_{3} 4}$.
Решение
$ {\log_{3} (9⋅4)} / {2+\log_{3}4} ={\log_{3} 9+\log_3 4} / {2+\log_{3}4} ={2+\log_3 4} / {2+\log_{3}4} =1$.
Ответ: 1
Показать решение
Полный курс
Задача 7
Найдите значение выражения $ \log_2 (\log_5 625)$.
Решение
$log_2(log_5 5^4) = log_2 4 = 2$.
Ответ: 2
Показать решение
Полный курс
Задача 8
Найдите значение выражения ${7^{\log_5 50}} / {7^{\log_{5}2 }}$.
Решение
${7^{log_5(2·25)}}/{7^{log_5 2}} = {7^{log_5 2+log_5 25}}/{7^{log_5 2}} = 7^{log_ 5 2+log_5 5^2 -log_ 5 2} = 7^2 = 49$.
Ответ: 49
Показать решение
Полный курс
Задача 9
Найдите значение выражения ${\log_7 23} / {\log_{49}23} $.
Решение
${\log_7 23} / {\log_{7^2}23} ={\log_7 23} / {{1} / {2}\log_{7 }23}=2$.
Ответ: 2
Показать решение
Полный курс
Задача 10
Найдите значение выражения ${15 \cos 19°} / {\cos341°}$.
Решение
Применив формулу приведения $cos(360° -α) = cosα$, получим ${15cos19°}/{cos(360° — 19°)} = {15cos19°}/{cos19°} = 15$.
Ответ: 15
Показать решение
Полный курс
Задача 11
Найдите значение выражения ${3 \cos 39°} / {\sin51°}$.
Решение
Применив формулу приведения $sin(90° -α) = cosα$, получим ${3cos39°}/{sin(90° — 39°)} = {3 cos 39°}/{cos 39°} = 3$.
Ответ: 3
Показать решение
Полный курс
Задача 12
Найдите значение выражения ${15√ {x}-3} / {√ {x}}+{3√ {x}} / {x}+2x-8$ при $x=3$.
Решение
${15√x}/{√x} — {3}/{√x} + {3√x}/{(√x)^2} + 2x — 8 = 15 — {3}/{√x} + {3}/{√x} + 2x — 8 = 7 + 2x$.
При $x = 3$ получим $7 + 2·3 = 13$.
Ответ: 13
Показать решение
Полный курс
Задача 13
Найдите значение выражения ${f(x+3)} / {f(x-3)}$, если $f(x)=5^x$.
Решение
$f(x)=5^x$ ${f(x+3)}/{f(x-3)}={5^{x+3}}/{5^{x-3}}=5^6=15 625$
Ответ: 15625
Показать решение
Полный курс
Задача 14
Найдите значение выражения $(√ {23} — √ {15})(√ {23}+√ {15})$.
Решение
$(√{23} — √{15})(√{23} + √{15}) = (√{23})^2 — (√{15})^2 = 23 — 15 = 8$.
Ответ: 8
Показать решение
Полный курс
Задача 15
Найдите значение выражения ${6^{3√2+2}·6^{2√2}}/{6^{5√2-1}}$.
Решение
${6^{3√2+2}·6^{2√2}}/{6^{5√2-1}}=6^{3√2+2+2√2-(5√2-1)} = 6^{5√2+2-5√2+1} = 6^3 = 216$.
Ответ: 216
Показать решение
Полный курс
Задача 16
Найдите значение выражения $8^{3√ {5}-1}⋅ 8^{1-√ {5} }: 8^{2√ {5}-1}$.
Решение
$8^{(3√5-1)+(1-√5)-(2√5-1)} = 8^1 = 8$.
Ответ: 8
Показать решение
Полный курс
Задача 17
Найдите значение выражения $6x⋅(2x^9)^4:{(4x^{12})}^3$ при $x=5$.
Решение
$6x·(2x^9)^4 : (4^3 · (x^{12})^3) = 6x · (2^4 · x^{36}) : ((2^2)^3 · x^{36}) = {6x · 2^4 · x^{36}}/{2^6·x^{36}} = {6x}/{4} = 1.5x$.При $х=5$, $1.5·х=1.5·5=7.5$
Ответ: 7.5
Показать решение
Полный курс
Задача 18
Найдите значение выражения $x⋅5^{2x+1}⋅ 25^{-x}$ при $x=3$.
Решение
$x⋅5^{2x+1}⋅ (5^2)^{-x}=x⋅5^{2x+1-2x}=x⋅5$. При $x=3$ получим $3⋅5=15$.
Ответ: 15
Показать решение
Полный курс
Решение
$tgβ={sinβ}/{cosβ}=-5$$ sinβ=-5cosβ$$ (3sinβ+15cosβ−8)/(sinβ+5cosβ+2)=(3⋅(-5cosβ)+15cosβ-8)/(-5cosβ+5cosβ+2)=(-15cosβ+15cosβ-8)/2=-8/2=-4$
Ответ: -4
Показать решение
Полный курс
Показать еще
Поиск точек экстремума
Теперь, когда мы разобрались, как не запутаться и понять, что необходимо найти в задаче, приступим к разбору самих заданий и алгоритмов к ним. Начнём с поиска точек экстремума. Чтобы провести анализ функции, необходимо определить основные этапы. У функции есть точки экстремума, в них производная равна нулю. Единственный способ, определить, является ли данная точка точкой максимума или минимума – это определить знаки производной до и после неё, если знак производной меняется с «–» на «+», то это будет точка минимума, а если с «+» на «–», то точка максимума. Таким образом общий порядок действий будет следующим:
Данному алгоритму подчиняются абсолютно все задания, в которых нужно найти точки экстремума.