Пример №4
Два кубика бросают одновременно. Найти вероятность выбросить 9 очков.
Решение: Подберем пары чисел от 1 до 6, которые в сумме дают 9
3+6
4+5
5+4
6+3
Понятно, что на первом кубике может выпасть 4 из 6 возможных чисел. Вероятность составляет: 4/6=2/3
При бросании второго кубика должно выпасть 1 число из 6, вероятность этого события 1/6.
Тогда вероятность того, что сумма очков составит 9, равна произведению вероятностей: 2/3*1/6=2/18=1/9=0,11
Ответ: 0,11.
Эту задачу можно решить с помощью таблицы, где в верхней строке указано число на перовом кубике, в левом столбце – число на втором, а в ячейках – их сумма. (Такую таблицу можно за минуту набросать на черновике)
Из таблицы видно, что из 36 возможных исходов, 9 очков выпадает в 4-х случаях. Т.е. вероятность составляет 4/36=1/9=0,11
Ответ: 0,11.
Показательные уравнения
Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.
$a^x=b$
При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n·a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n∙m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби
$a^{-n}={1}/{a^n}$
${a^{-n}}/{b^{-k}}={b^k}/{a^n}$
8. Радикал (корень) можно представить в виде степени с дробным показателем
$√^n{a^k}=a^{{k}/{n}}$
Виды показательных уравнений:
1. Простые показательные уравнения:
а) Вида $a^{f(x)}=a^{g(x)}$, где $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием ($а >0, a≠1$) равны только тогда, когда равны их показатели.
$f(x)=g(x)$
b) Уравнение вида $a^{f(x)}=b, b>0$
Для решения таких уравнений надо обе части прологарифмировать по основанию $a$, получается
$log_{a}a^{f(x)}=log_{a}b$
$f(x)=log_{a}b$
2. Метод уравнивания оснований.
3. Метод разложения на множители и замены переменной.
- Для данного метода во всем уравнении по свойству степеней надо преобразовать степени к одному виду $a^{f(x)}$.
- Сделать замену переменной $a^{f(x)}=t, t > 0$.
- Получаем рациональное уравнение, которое необходимо решить путем разложения на множители выражения.
- Делаем обратные замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^{f(x)}=t$, решаем его и результат записываем в ответ.
Пример:
Решите уравнение $2^{3x}-7·2^{2x-1}+7·2^{x-1}-1=0$
Решение:
По свойству степеней преобразуем выражение так, чтобы получилась степень 2^x.
$(2^x)^3-{7·(2^x)^2}/{2}+{7·2^x}/{2-1}=0$
Сделаем замену переменной $2^x=t; t>0$
Получаем кубическое уравнение вида
$t^3-{7·t^2}/{2}+{7·t}/{2}-1=0$
Умножим все уравнение на $2$, чтобы избавиться от знаменателей
$2t^3-7·t^2+7·t-2=0$
Разложим левую часть уравнения методом группировки
$(2t^3-2)-(7·t^2-7·t)=0$
Вынесем из первой скобки общий множитель $2$, из второй $7t$
$2(t^3-1)-7t(t-1)=0$
Дополнительно в первой скобке видим формулу разность кубов
$2(t-1)(t^2+t+1)-7t(t-1)=0$
Далее скобку $(t-1)$ как общий множитель вынесем вперед
$(t-1)(2t^2+2t+2-7t)=0$
Произведение равно нулю, когда хотя бы один из множителей равен нулю
1) $(t-1)=0;$ 2) $2t^2+2t+2-7t=0$
Решим первое уравнение
$t_1=1$
Решим второе уравнение через дискриминант
$2t^2-5t+2=0$
$D=25-4·2·2=9=3^2$
$t_2={5-3}/{4}={1}/{2}$
$t_3={5+3}/{4}=2$
Получили три корня, далее делаем обратную замену и получаем три простых показательных уравнения
$2^x=1; 2^x={1}/{2}; 2^x=2$
$2^x=2^0; 2^x=2^{-1}; 2^x=2^1$
$х_1=0; х_2=-1; х_3=1$
Ответ: $-1; 0; 1$
4. Метод преобразования в квадратное уравнение
- Имеем уравнение вида $А·a^{2f(x)}+В·a^{f(x)}+С=0$, где $А, В$ и $С$ — коэффициенты.
- Делаем замену $a^{f(x)}=t, t > 0$.
- Получается квадратное уравнение вида $A·t^2+B·t+С=0$. Решаем полученное уравнение.
- Делаем обратную замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^{f(x)}=t$, решаем его и результат записываем в ответ.
Способы разложения на множители:
Вынесение общего множителя за скобки.
Чтобы разложить многочлен на множители путем вынесения за скобки общего множителя надо:
- Определить общий множитель.
- Разделить на него данный многочлен.
- Записать произведение общего множителя и полученного частного (заключив это частное в скобки).
Пример:
Разложить на множители многочлен: $10a^{3}b-8a^{2}b^2+2a$.
Общий множитель у данного многочлена $2а$, так как на $2$ и на «а» делятся все члены. Далее найдем частное от деления исходного многочлена на «2а», получаем:
$10a^{3}b-8a^{2}b^2+2а=2a({10a^{3}b}/{2a}-{8a^{2}b^2}/{2a}+{2a}/{2a})=2a(5a^{2}b-4ab^2+1)$
Это и есть конечный результат разложения на множители.
Пример №8
К зачету надо выучить 10 вопросов. Саша выучил 2, а остальные только прочитал. Если Саше попадется выученный билет, то он сдаст зачет с вероятностью 0,9. Если Саше попадется вопрос, который он только прочитал, то вероятность сдать зачет 0,3. Вопросы на зачете распределяются случайным образом. Найти вероятность того, что Саша сдаст зачет.
Решение: Из 10 билетов выучены 2, не выучены 8. Вероятность получить выученный вопрос 2/10, вероятность получить не выученный вопрос 8/10.
Вероятность сдать зачет по выученному билету: 2/10*0,9=0,18
Вероятность сдать по невыученному билету: 8/10*0,3=0,24
Итоговая вероятность: 0,18+0,24=0,42
Ответ: 0,42.
Квадратная решетка и координатная плоскость
В задании №3 профильного уровня ЕГЭ по математике мы будем работать с фигурами на квадратных решетках — вычислять параметры фигур — стороны или площади, а также расстояния между точками. Приступим непосредственно к разбору типовых вариантов.
Первый вариант задания (демонстрационный вариант 2018)
На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите площадь.
Алгоритм решения:
- Подсчитываем длину основания и высоты.
- Записываем формулу вычисления площади.
- Вычисляем площадь.
- Записываем ответ.
Решение:
1. Подсчитываем длины основания и высоты:
основание = 6,
высота = 2.
2. Записываем формулу площади треугольника: S= ah|2.
3. Вычисляем площадь: S= 6∙2/2=6
Ответ: 6.
Второй вариант задания (из Ященко, №1)
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
Алгоритм решения:
- Подсчитываем длину каждого основания и высоты трапеции.
- Записываем формулу длины средней линии трапеции.
- Вычисляем среднюю линию.
- Записываем ответ.
Решение:
1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 3, большее – 4.
2. Длина средней линии трапеции находится по формуле
, где a и b – длина верхнего и нижнего оснований трапеции.
3. Имеем:
.
4. Значит, средняя линия равна 3,5.
Ответ: 3,5.
Третий вариант задания (из Ященко, №2)
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
Алгоритм решения:
- Подсчитываем длину каждого основания и высоты трапеции.
- Записываем формулу длины средней линии трапеции.
- Вычисляем среднюю линию.
- Записываем ответ.
Решение:
1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 2, большее – 6.
2. Длина средней линии трапеции находится по формуле
, где a и b – длина верхнего и нижнего оснований трапеции.
3. Имеем: 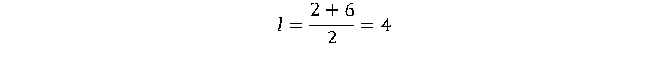
4. Значит, средняя линия равна 4.
Ответ: 4.
Четвертый вариант задания (из Ященко, №4)
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины В.
Алгоритм решения:
- Проведем перпендикуряры из вершин Аи С.
- Построим биссектрису угла В.
- Покажем, что биссектриса параллельна высотам.
- Измерим длину биссектрисы.
- Запишем ответ.
Решение:
1. Проведем из вершин А и С отрезки АВ1 иСВ2, перпендикулярные прямой, содержащей вершину В на рисунке.
2. Построим биссектрису угла B.
3. Рассмотрим треугольники АВВ1 иВВ2С. Они прямоугольные, тогда из соотношений в прямоугольных треугольниках
Это означает, что углы АВB1 и СВB2 равны, так как равны тангенсы этих углов.
Раз равны углы, то стороны AB и BC расположены под одним углом относительно вертикали (На рисунке она проведена синим). Эта вертикаль является биссектрисой. Длина биссектрисы по рисунку равна 3.
Ответ: 3.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Алгоритм решения:
- Рассмотрим рисунок и измерим основания.
- Проведем высоту.
- Запишем формулу площади трапеции.
- Вычислим площадь по формуле.
Решение:
1. На рисунке основания равны 3 и 8.
2. Опустим высоту. Она рана 3.
3. Формула трапеции: S=h(a+b)/2, где a,b – основания, h – высота.
4. Вычислим площадь, подставив значения: S=3∙(3+8)/2=16,5
Следовательно, площадь данной трапеции равна 16,5.
Ответ: 16,5.
Несколько советов по решению 2 задания
Сложнее всего определить, когда вероятности двух событий надо перемножать, а когда складывать. Попадаются задачи, когда надо сделать и то, и другое. Если вы нашли вероятности отдельных событий, но не можете определиться, что с ними делать дальше – доверьтесь интуиции.
Если вы понимаете что вероятность двух событий больше, чем вероятность каждого в отдельности – складывайте. (Например, вероятность выбросить решку на одной из двух монет очевидно больше, чем выбросить решку на одной монете.)
Если вероятность двух событий меньше, чем каждого в отдельности – перемножайте. (Например, вероятность выбросить решку на обеих монетах меньше, чем вероятность выбросить решку на одной из них.)
Понятно, что интуиция – подход ненаучный. Но на ЕГЭ в задании с кратким ответом лучше дать какой-нибудь ответ, чем не дать никакого.
Однако не забывайте, что профильный ЕГЭ по математике является не только выпускным, но и вступительным испытанием. Большинство школьных задач на вероятность можно решить путем логических рассуждений. Это создает иллюзию легкости теории вероятности и математической статистики. Но на самом деле это одна из самых передовых и востребованных областей математики, и в ВУЗе вы ощутите её сложность в полной мере.
Рекомендуем также ознакомиться с разбором , и задания.
Решение заданий 3 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube: 
Задания с базами данных
3_6: 3 (ранее 4) задание ЕГЭ или 5 задание ГВЭ 11 класс по информатике 2018 (ФИПИ):
Ниже представлены две таблицы из базы данных. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1.
Определите на основании приведённых данных фамилию и инициалы племянника Геладзе П.П.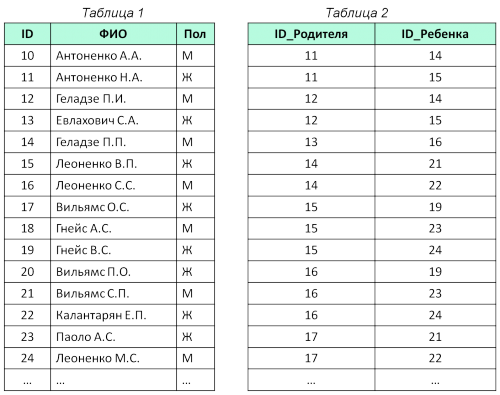
Варианты ответа:
1) Вильямс С.П.
2) Геладзе П.И.
3) Леоненко М.С.
4) Леоненко С.С.
Решение:
Результат: 3
Подробное решение задания ГВЭ смотрите в видеоуроке:
https://youtube.com/watch?v=CtwcLEUFxKw
3_1: ЕГЭ по информатике 2017 задание 3 ФИПИ вариант 1:
Ниже представлены две таблицы из базы данных. Каждая строка Таблицы 2 содержит информацию о ребенке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке Таблицы 1.
Определите на основании приведенных данных суммарное количество прямых потомков (т.е. детей, внуков, правнуков) Иоли А.Б.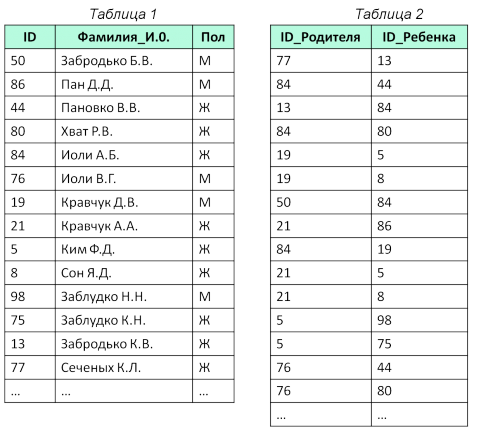
Решение:
- В первой таблице находим Иоли А.Б, ей соответствует ID 84
- Все остальное решение будет связано со второй таблицей: будем в ней искать ID родителя и соответствующего ему ID ребенка.
- Выполним задание при помощи дерева, подробно рассматривая каждый уровень иерархии: сначала детей родителя 84, затем по полученным ID — найдем внуков Иоли А.Б, затем правнуков и т.д.
Посчитаем количество потомков: их 7
Результат: 7
Также можно посмотреть видео решения 3 задания ЕГЭ по информатике:
https://youtube.com/watch?v=qmLQzAS9Z5E
3_2: ЕГЭ по информатике 2017 задание 3 ФИПИ вариант 9:
Ниже представлены две таблицы из базы данных, в которых собраны сведения о сотрудниках некоторой организации. Каждая строка Таблицы 2 содержит информацию о сотруднике структурного подразделения и о его непосредственном руководителе, который, в свою очередь, является непосредственным подчиненным руководителя более высокого уровня. Информация представлена значением поля ID в соответствующей строке Таблицы 1.
Определите на основании приведенных данных суммарное количество подчиненных (непосредственных и через руководителей более низкого уровня) Сидорова Т.И.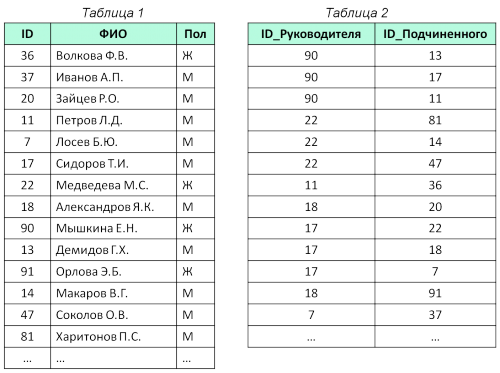
Решение:
- В первой таблице находим Сидорова Т.И., ему соответствует ID 17
- Все остальное решение будет связано со второй таблицей: будем в ней искать ID руководителя и соответствующих ему ID подчиненных.
- Выполним задание при помощи дерева, подробно рассматривая каждый уровень иерархии: сначала непосредственных подчиненных руководителя 17, затем по полученным ID — найдем подчиненных подчиненных и т.д.
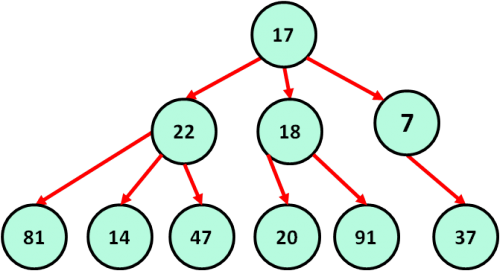
Посчитаем количество подчиненных: 9
Результат: 9
Можете ознакомиться с решением данного 3 задания ЕГЭ по информатике из видеоурока:
https://youtube.com/watch?v=aE2LHa6WUGo
3_4: Демоверсия ЕГЭ 2018 информатика (ФИПИ):
Ниже представлены два фрагмента таблиц из базы данных о жителях микрорайона. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1.
Определите на основании приведённых данных, у скольких детей на момент их рождения матерям было больше 22 полных лет. При вычислении ответа учитывайте только информацию из приведённых фрагментов таблиц.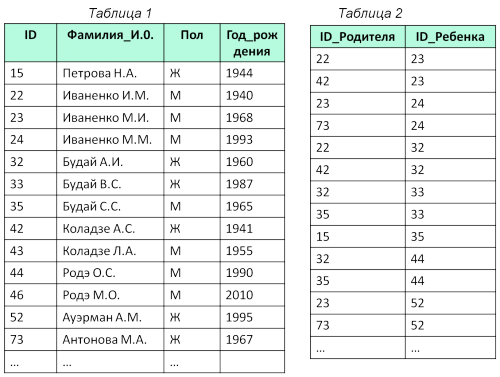
Решение:
ID 23: 1968 - 1941 = 27 ! 24: 1993 - 1967 = 26 ! 32: 1960 - 1941 = 19 33: 1987 - 1960 = 27 ! 35: 1965 - 1944 = 21 44: 1990 - 1960 = 30 ! 52: 1995 - 1967 = 28 !
Условию соответствует 5 пунктов ().
Результат: 5
Подробное решение данного 3 (раньше № 4) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
https://youtube.com/watch?v=quzYvHT7V3k
Применение формул сокращенного умножения
1. Квадрат суммы раскладывается на квадрат первого числа плюс удвоенное произведение первого числа на второе число и плюс квадрат второго числа.
$(a+b)^2=a^2+2ab+b^2$
2. Квадрат разности раскладывается на квадрат первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа.
$(a-b)^2=a^2-2ab+b^2$
3. Разность квадратов раскладывается на произведение разности чисел и их сумму.
$a^2-b^2=(a+b)(a-b)$
4. Куб суммы равен кубу первого числа плюс утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа плюс куб второго числа.
$(a+b)^3=a^3+3a^2b+3ab^2+b^3$
5. Куб разности равен кубу первого числа минус утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа и минус куб второго числа.
$(a-b)^3=a^3-3a^2b+3ab^2-b^3$
6. Сумма кубов равна произведению суммы чисел на неполный квадрат разности.
$a^3+b^3=(a+b)(a^2-ab+b^2)$
7. Разность кубов равна произведению разности чисел на неполный квадрат суммы.
$a^3-b^3=(a-b)(a^2+ab+b^2)$
Логарифмические уравнения
Логарифмическими уравнениями называют уравнения вида $log_{a}f(x)=log_{a}g(x)$, где $а$ – положительное число, отличное от $1$, и уравнения, сводящиеся к этому виду.
Для решения логарифмических уравнений необходимо знать свойства логарифмов: все свойства логарифмов мы будем рассматривать для $a > 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.
1. Для любых действительных чисел $m$ и $n$ справедливы равенства:
$log_{а}b^m=mlog_{a}b;$
$log_{a^m}b={1}/{m}log_{a}b.$
$log_{a^n}b^m={m}/{n}log_{a}b$
Пример:
$log_{3}3^{10}=10log_{3}3=10;$
$log_{5^3}7={1}/{3}log_{5}7;$
$log_{3^7}4^5={5}/{7}log_{3}4;$
2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.
$log_a(bc)=log_{a}b+log_{a}c$
3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию
$log_{a}{b}/{c}=log_{a}b-log_{a}c$
4. При умножении двух логарифмов можно поменять местами их основания
$log_{a}b∙log_{c}d=log_{c}b∙log_{a}d$, если $a, b, c$ и $d > 0, a≠1, b≠1.$
5. $c^(log_{a}b)=b^{log_{a}b}$, где $а, b, c > 0, a≠1$
6. Формула перехода к новому основанию
$log_{a}b={log_{c}b}/{log_{c}a}$
7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение
$log_{a}b={1}/{log_{b}a}$
Можно выделить несколько основных видов логарифмических уравнений:
— Простейшие логарифмические уравнения: $log_{a}x=b$. Решение данного вида уравнений следует из определения логарифма, т.е. $x=a^b$ и $х > 0$
Пример:
$log_{2}x=3$
Представим обе части уравнения в виде логарифма по основанию $2$
$log_{2}x=log_{2}2^3$
Если логарифмы по одинаковому основанию равны, то подлогарифмические выражения тоже равны.
$x = 8$
Ответ: $х = 8$
— Уравнения вида: $log_{a}f(x)=log_{a}g(x)$. Т.к. основания одинаковые, то приравниваем подлогарифмические выражения и учитываем ОДЗ:
$\table\{\ f(x)=g(x);\ f(x)>0;\ g(x) > 0, а > 0, а≠1;$
Пример:
$log_{3}(x^2-3x-5)=log_{3}(7-2x)$
Т.к. основания одинаковые, то приравниваем подлогарифмические выражения
$x^2-3x-5=7-2x$
Перенесем все слагаемые в левую часть уравнения и приводим подобные слагаемые
$x^2-x-12=0$
$x_1=4,x_2= -3$
Проверим найденные корни по условиям $\table\{\ x^2-3x-5>0;\ 7-2x>0;$
При подстановке во второе неравенство корень $х=4$ не удовлетворяет условию, следовательно, он посторонний корень
Ответ: $х=-3$
Метод замены переменной.
В данном методе надо:
- Записать ОДЗ уравнения.
- По свойствам логарифмов добиться того, чтобы в уравнении получились одинаковые логарифмы.
- Заменить $log_{a}f(x)$ на любую переменную.
- Решить уравнение относительно новой переменной.
- Вернутся в п.3, подставить вместо переменной значение и получить простейшее уравнение вида: $log_{a}x=b$
- Решить простейшее уравнение.
- После нахождения корней логарифмического уравнения необходимо поставить их в п.1 и проверить условие ОДЗ.
Пример:
Решите уравнение $log_{2}√x+2log_{√x}2-3=0$
Решение:
1. Запишем ОДЗ уравнения:
$\table\{\ х>0,\text»так как стоит под знаком корня и логарифма»;\ √х≠1→х≠1;$
2. Сделаем логарифмы по основанию $2$, для этого воспользуемся во втором слагаемом правилом перехода к новому основанию:
$log_{2}√x+{2}/{log_{2}√x}-3=0$
3. Далее сделаем замену переменной $log_{2}√x=t$
4. Получим дробно — рациональное уравнение относительно переменной t
$t+{2}/{t}-3=0$
Приведем все слагаемые к общему знаменателю $t$.
${t^2+2-3t}/{t}=0$
Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
$t^2+2-3t=0$, $t≠0$
5. Решим полученное квадратное уравнение по теореме Виета:
$t^2-3t+2=0$
$t_1=1; t_2=2$
6. Вернемся в п.3, сделаем обратную замену и получим два простых логарифмических уравнения:
$log_{2}√x=1$, $log_{2}√x=2$
Прологарифмируем правые части уравнений
$log_{2}√x=log_{2}2$, $log_{2}√x=log_{2}4$
Приравняем подлогарифмические выражения
$√x=2$, $√x=4$
Чтобы избавиться от корня, возведем обе части уравнения в квадрат
$х_1=4$, $х_2= 16$
7. Подставим корни логарифмического уравнения в п.1 и проверим условие ОДЗ.
$\{\table\ 4 >0; \4≠1;$
Первый корень удовлетворяет ОДЗ.
$\{\table\ 16 >0; \16≠1;$ Второй корень тоже удовлетворяет ОДЗ.
Ответ: $4; 16$
Уравнения вида $log_{a^2}x+log_{a}x+c=0$. Такие уравнения решаются способом введения новой переменной и переходом к обычному квадратному уравнению. После того, как корни уравнения будут найдены, надо отобрать их с учетом ОДЗ.
Объяснение заданий 3 ЕГЭ по информатике
3-е задание: «Реляционные базы данных»Уровень сложности — базовый,Требуется использование специализированного программного обеспечения — нет,Максимальный балл — 1,Примерное время выполнения — 3 минуты.
Проверяемые элементы содержания: Знание о технологии хранения, поиска и сортировки информации в реляционных базах данных
До ЕГЭ 2021 года — это было задание № 4 ЕГЭ
* Некоторые изображения страницы взяты из материалов презентации К. Полякова
Для решения задания 3 ЕГЭ необходимо рассмотреть тему предыдущего урока — (деревья).
Иногда также попадаются задания, которые требуют знаний основ алгебры логики.
Базы данных
База данных – это хранилище больших объемов данных некоторой предметной области, организованное в определенную структуру, т.е. хранящихся в упорядоченном виде.
Задания ЕГЭ в основном связаны с табличными базами данных, поэтому мы их кратко и рассмотрим.
Данные в табличных БД представлены, соответственно, в виде таблицы.
Строки таблицы носят название записи, а столбцы — поля: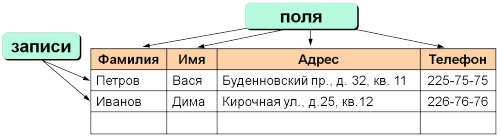
- Абсолютно все поля должны быть снабжены уникальными именами. В примере: Фамилия, Имя, Адрес, Телефон.
- Поля имеют различные типы данных, в зависимости от их содержимого (например, символьный, целочисленный, денежный и т.п.).
- Поля могут быть обязательными для заполнения или нет.
- Таблица может иметь безграничное количество записей.
Ключевое поле – это поле, которое однозначно определяет запись.
В таблице не может быть двух и более записей с одинаковым значением ключевого поля (ключа).
- Для выбора ключевого поля берутся какие-либо уникальные данные об объекте: например, номер паспорта человека (второго такого номера ни у кого нет).
- Если в таблице не предусмотрены такие уникальные поля, то создается так называемый суррогатный ключ — поле (обычно ID или Код) с уникальными номерами — счетчик — для каждой записи в таблице.
Реляционная база данных – это совокупность таблиц, которые связываются между собой (между которыми устанавливаются отношения). Связь создается с помощью числовых кодов (ключевых полей).
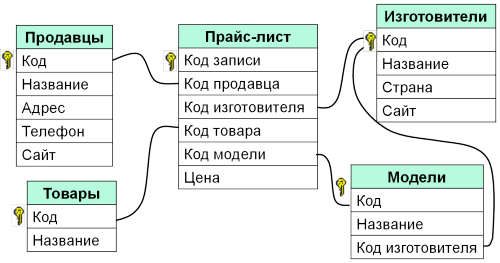
Реляционная БД «Магазин»
Положительное в реляционных БД:
- исключено дублирование информации;
- если изменяются какие-либо данные, к примеру, адрес фирмы, то достаточно изменить его только в одной таблице — Продавцы;
- защита от неправильного ввода (или ввода с ошибками): можно выбрать (как бы ввести) только фирму, которая есть в таблице Продавцы;
- Для удобства осуществления поиска в базе данных часто создается специальная таблица Индексы.
- Индекс – это специальная таблица, предназначенная для осуществления быстрого поиска в основной таблице по выбранному столбцу.
Последовательность выполнения логических операций в сложных запросах:
сначала выполняются отношения, затем – «И», потом – «ИЛИ». Чтобы изменить порядок выполнения используются скобки.
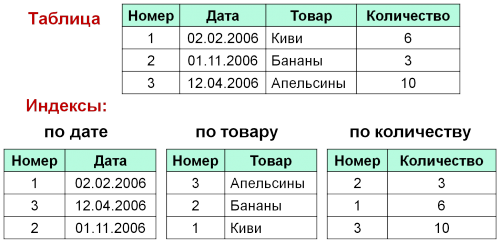
Индексы
Файловая система
* тема с масками скорее всего не будет представлена на ЕГЭ 2021 года
- файлы на диске хранятся в так называемых каталогах или папках;
- каталоги организованы в иерархическую структуру — дерево каталогов;
- главный каталог диска называется корневым каталогом и обозначается буквой логического диска, за которой следует двоеточие и знак «\» (обратный слэш); например, A:\ – это обозначение корневого каталога диска А.
Дерево каталогов
каждый каталог (кроме корневого) имеет один единственный «родительский» каталог – это тот каталог, внутри которого и располагается данный каталог
полный адрес каталога – это перечисление всех каталогов, в которые нужно войти, чтобы попасть в данный каталог (начиная с корневого каталога диска); например
— полный путь каталога SCHOOL
полный адрес файла состоит из адреса каталога, в котором он находится, символа и имени файла, например
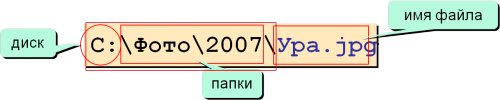
Полный путь файла
маска — выделение группы файлов по их именам; имена этих файлов имеют общие свойства, например, одинаковое расширение
в масках, кроме стандартных символов используются два специальных символа: звездочка «*» и знак вопроса «?»;
- звездочка «*» обозначает любое количество любых символов, в том числе, может обозначать 0 символов;
- знак вопроса «?» обозначает ровно один любой символ.

Примеры масок файлов
Сравнение строковых данных
В задачах 3-го типа часто приходится сравнивать строковые значения. Посмотрим, как правильно это делать: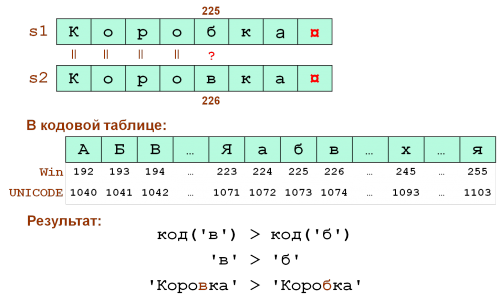
Любой символ всегда больше пустого: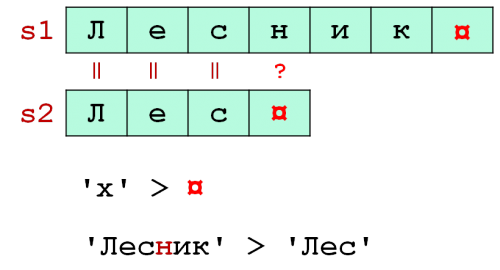
Егифка :