Как сдать базовую математику на максимум? разбор заданий

Развивайте математическое мышление

В некоторых заданиях быстрее и проще не проводить долгих вычислений, а прикинуть или догадаться, каков верный ответ. Но после этого, разумеется, надо выполнить проверку. Так вы экономите время и развиваете математическое мышление и эрудицию.

Задание 16: текстовая задача

Для начала мы вводим неизвестное: х деталей в час делает второй рабочий. Тогда х+4 детали в час делает первый рабочий. Известно, что 140 деталей первый рабочий делает на 4 часа быстрее, чем второй. Составляем уравнение:

Решаем и получаем выражение х(x+4)=140. Внимательно присмотритесь к этому равенству. Вам необходимо найти такое значение х, при котором произведение двух чисел, отличающихся на 4, будет равно 140. Не обязательно считать, можно просто увидеть, что это 10 и 14.

Ответ на задачу: х=10.

Чтобы развить в себе подобное математическое видение, достаточно решать как можно больше задач и не обращаться к калькулятору сразу же, как только надо что-то посчитать.

Задание 6: арифметика в жизни

Здесь тоже гораздо быстрее не делить с остатком, а прикинуть, сколько автобусов может понадобиться, а затем выполнить простую операцию умножения.

В данном случае нам надо перевести 274 человека, а в автобус влезает 46. Возьмем для начала цифру 6 и умножим на 46, получилось 276 человек. Это значит, что мы нашли правильный ответ, не углубляясь в сложные расчеты.

Задание 18 (Делаем обязательно!)

Задача проверяет у ребят, которые хотят сдать базовую математику, умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.

Все,
что от вас требуется – схематично изобразить на черновике ясень, рябину и
осину, указать известную разницу в высоте и внимательно сопоставить картинку с
утверждениями.

Ответ:
14

Важно! Не
додумывайте какие-то дополнительные условия, не указанные в тексте задачи.
Учитесь читать строго то, что написано. А
бывают случаи, когда с визуализацией задачки придется постараться

А
бывают случаи, когда с визуализацией задачки придется постараться.

Тут
иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет
наглядно изобразить множество объектов. В данном случае — школьников. Давайте
прикинем, как ребята могут распределиться по кружкам?

Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем, 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.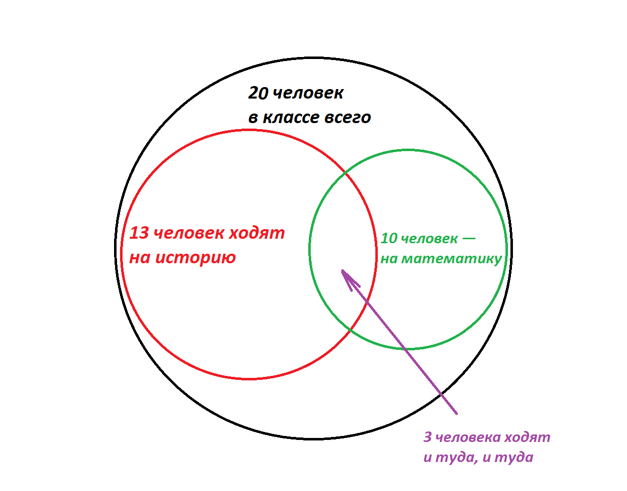
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.

Конечно, возможны еще какие-то промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.

Смотрим на первую картинку. Даже если все ребята будут
очень стараться посетить оба кружка, они ограничены условиями задачи, и
максимум на оба попадут 10 человек из 20. НЕТ.
Тут надо рассмотреть другую крайность, которую мы
изобразили на второй картинке. Как бы ребята не старались не встречаться на
кружках, хотя бы трое попадут на оба сразу. ДА.
Уж точно неверно. На обеих наших картинках есть
ребята, которые ходят на историю, но не ходят на математику. НЕТ.
Смотрим на первую картинку. Максимум оба кружка могут
посещать 10 человек. ДА.

Ответ: 24.

Так что для решения иногда мало логики, понадобится
еще чуток воображения. Потренируйтесь, и ваши шансы получить балл повысятся.

Советы по подготовке

Вспомните теорию

Прежде чем приступать к решению задач, повторите все формулы, определения, понятия и законы. Вспомните простые темы, которые вы могли забыть к выпускному классу, а потом уже беритесь за сложный и неосвоенный материал. Так вам будет легче справляться с заданиями, когда вы перейдёте к практике.

Научитесь считать без калькулятора

Некоторые задачи экзамена требуют навыка быстрого счёта. К тому же, на ЕГЭ вам нужно выделить побольше времени на решение сложных задач и проверку ответов. Будьте уверены: вы не пожалеете, если научитесь. Это умение пригодится вам не только на экзамене, но и в жизни.

Внимательно читайте текст заданий

Приступайте к решению только после того, как убедитесь, что поняли задание правильно. Смотрите, в каких единицах измерения нужно дать ответ и требуется ли его округлять. Такой подход убережёт вас от множества мелких ошибок.

Проверяйте свои знания

Демоверсии ЕГЭ и тесты вы можете найти на сайте ФИПИ. Или зарегистрируйтесь на нашем портале и получите доступ к нашей библиотеке знаний с полезными материалами для подготовки.

Не забывайте отдыхать

Сдать экзамен, несомненно, важно, и для этого нужно потратить много времени на подготовку. Однако она не будет эффективной, если вы перестанете хорошо спать, гулять на свежем воздухе, заниматься любимым хобби и общаться с друзьями

Обязательно отведите время на отдых — тогда подготовка к ЕГЭ по базовой математике пройдёт с пользой, и вы точно справитесь на отлично.

Когда и с чего начинать подготовку

Базовый уровень ЕГЭ по математике включает в себя общие школьные знания, года подготовки будет достаточно. Определите свой уровень знаний с помощью теста или на занятии с преподавателем. Например, в нашей онлайн-школе вводный урок бесплатный. На нём вы узнаете, что помните хорошо, а что нужно повторить, и составите план занятий.

Если на данный момент ваш уровень подготовки слабый, создайте себе хорошую базу. Вспомните свойства степеней, корней и логарифмов. Повторите типы уравнений и методы их решения

Уделите внимание геометрии: можно начать с треугольника, синусов и косинусов. Сделать всё это тоже будет легче с опытным репетитором

Задание 10 (Делаем обязательно!)

Простая задача на определение вероятности.

Решаем с помощью формулы:

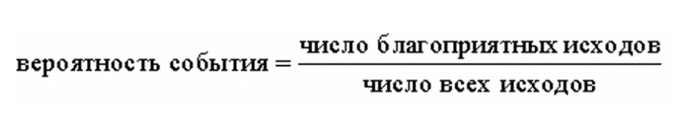
Внимательно читаем вопрос: спрашивают вероятность купить исправную
лампочку. Если из ста 3 неисправны, значит остальные в порядке, и нам подойдет
любая из оставшихся 97 штук. Это и есть наши благоприятные исходы из формулы.

Ответ: 0,97.

Будьте внимательны: иногда в задаче есть указание к округлению. Значит ответ
у вас выйдет некрасивый, но вы его «причЕшите» округлением.

Еще один подвох: формулировка с предлогом «на». К примеру, «на 100
лампочек 3 неисправны, найдите вероятность купить неисправную». Подходящие
исходы даны тут явно: 3 неисправные лампочки. А вот число всех исходов спрятано
и составляет 103, потому что «на».

Всегда есть вероятность, что вам не повезет, и попадется задачка с
перебором подходящих вариантов… Тема довольно объемная, можете изучить ее
самостоятельно или надеяться на удачу.

Задание 6 (Делаем обязательно!)

Проверяется
ваше умение разделить случаи, когда требуется округлить величину в большую
сторону, а когда — в меньшую.

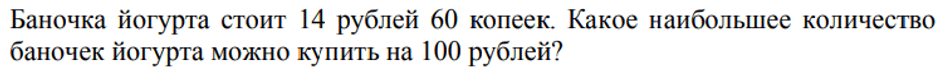
Если
ходите в магазин с карманными деньгами, то сталкиваетесь с подобными задачами
каждый день! Разделим 100 рублей на стоимость одной упаковки йогурта. Не
забываем приводить все величины к одной размерности:

100 : 14,6 = 6, 849…

Так сколько баночек йогурта вам продадут? На 7 штук
вам явно не хватает денег, значит округлить полученную величину надо до целого
в меньшую сторону. Математическое правило округление в этой задаче не
поможет.

Ответ: 6.

Одна пачка на 6 рулонов, значит на 63 рулона:

63 : 6 = 10,5

Но опять же, никто полпачки вам не продаст. Включаем
логику: возьмем меньше — не хватит еще половины пачки на 3 последние рулона.
Значит округлить надо в большую сторону, взять клей с небольшим запасом.
Снова математическое правило округления игнорируем.

Ответ: 11.

Задание 7 (Делаем обязательно!)

Хотите сдать базовую математику — вам повезло! В номере с уравнениями не попадется тригонометрического. Зато могут быть..

Линейные уравнения

Раскрываем
скобки, если они есть, слагаемые с «х» переносим в одну сторону от равно, без
«х» — в другую. Приводим подобные и решаем простейшее уравнение.

Квадратные уравнения

Бывают
полные и неполные, всего надо повторить 3 алгоритма решения! А формула
дискриминанта еще и в справочных материалах есть.

Иррациональные уравнения

Это
те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в
квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых
значений (ОДЗ): подставьте полученные корни в исходное уравнение и проверьте,
выполняется ли равенство. Если нет, то подставленное значение решением не
будет.

Показательные уравнения

Чуть
веселее. Ваша задача — с помощью формул свойств степеней привести уравнение к
виду, когда слева и справа от равно в основании степени будет одно и то же
число. После приравниваем показатели и решаем. Вот так:

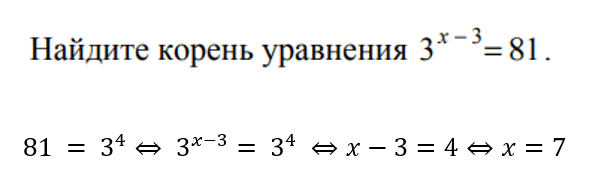
Ответ:
7.

Логарифмические уравнения

Еще
чуть веселее. С помощью формул свойств логарифмов приводим уравнение к виду,
когда слева и справа от равно будет логарифм с одинаковым основанием. После
приравниваем выражения под логарифмом и решаем.

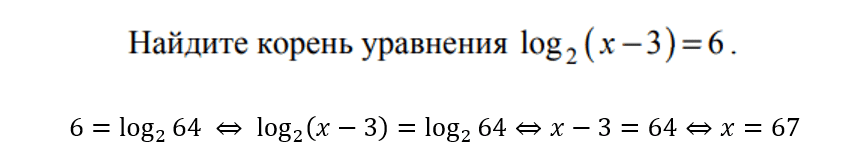
Тут тоже могут быть особенности с ОДЗ. Проверяйте
подстановкой.

Ответ: 67

Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо икса в уравнение! Не забывайте проверять, ведь это возможность убедиться на 100%, что заветный балл не проплывет мимо. Только так можно уверенно сдать базовую математику.

Разбор заданий ЕГЭ по базовой математике

Когда в школах начинается подготовка к ЕГЭ по математике, базовый уровень предмета просто нарешивают, не пытаясь разобрать задания. Чтобы разобраться в решении номеров, следует помнить основные типы встречающихся задач:

Текстовые задачи — сюда входят задачи на проценты, округление и смелкалку. Задачи на проценты решаются через умножение (процент принимается за десятичную дробь — 15% = 0,15). Задачи на округление решаются через деление с помощью логики. Задача №20 решается методом подбора.
Вычисления и преобразования — блок заданий, проверяющих умение обращаться с дробями и степенями, а также с тригонометрическими и иррациональными выражениями. Предполагается, что когда начинается подготовка к ЕГЭ по математике, базовый уровень знаний и умение обращаться с формулами, данными в начале КИМ, у вас уже имеется

В заданиях важно уметь подставлять необходимые значения в формулы и производить вычисления по этим формулам, а также записывать числа в разных видах.
Размеры и единицы измерения — чтобы решить задания этого раздела, необходимо знать порядок возрастания величин времени, длины, массы, объема, площади и уметь сопоставлять их с реальными объектами.
Фигуры — для решения заданий данного блока нужно знать основные понятия (единицы измерения и части фигур), а также уметь сопоставлять их с реальными фигурами и использовать эти данные при решении задач. Например, когда идет подготовка к ЕГЭ по математике, базовый уровень владения стереометрией должен позволять определить объем фигур, площадь их боковых граней и тому подобное.
Анализ информации — на экзамене информация представлена в виде графиков, диаграмм и текста

Для решения заданий нужно пронаблюдать за изменениями величин, а также найти наибольшую из них. Проверяется умение анализировать информацию или выбирать оптимальный вариант, опираясь на логическое мышление.
Уравнения и неравенства — проверяется умение использовать данные формулы, выводить из них другие, а также отмечать значения на числовой прямой. Все это обеспечит хорошая подготовка к ЕГЭ по математике: базовый уровень заданий раздела предполагает, что они с большей вероятностью будут типовыми и без подводных камней, к которым привыкают выпускники, сдающие профиль, и учителя.
Теория вероятностей (1 задание) — задание, решающееся с помощью определения нужной формулы комбинаторики (их всего три) и подставления в нее значений из задачи.

Задание 19

Чем дальше, тем интереснее становятся задачи. Этот номер уже напоминает олимпиадную задачку, правда для средней школы.

Если хотите сдать базовую математику и решить 19 номер, надо немного познакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте, если время на ЕГЭ позволяет.

Например,
тут нам помогут признаки делимости. Отдельного признака для 12 нет, потому нам
надо разложить его на разные множители, признак для которых есть.
Например, это:

3: чтобы
число делилось на 3, надо, чтобы сумма его цифр делилась на 3;
4: чтобы
число делилось на 4, надо, чтобы число, образованное последними двумя цифрами,
делилось на 4.

Начнем
с признака для четырех. Пока что наше число заканчивается на 13. На 4 не
делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на
61. Тоже не подходит. Вычеркнем еще одну. Теперь на конце 76… Вот оно! От
изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать
одну.

Теперь
проверим признак для трех: 7+5+1+5+7+6 = 31. Какое ближайшее число разделиться
на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.

Ответ: 75576. Конечно, это не единственное решение.

А
задание такого типа можно попытаться подобрать, расположений не слишком много.
Мы все же постараемся порассуждать, чтобы уменьшить количество возможных
вариантов.

Чтобы
число делилось на 10, оно должно заканчиваться на 0. Например, это получится,
если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под
условие задачи подойдет 7 + 27 + 356 = 390.

Ответ:
390.

Внимательно читайте условие

Нужно правильно понять, что именно спрашивают, а это не всегда очевидно.

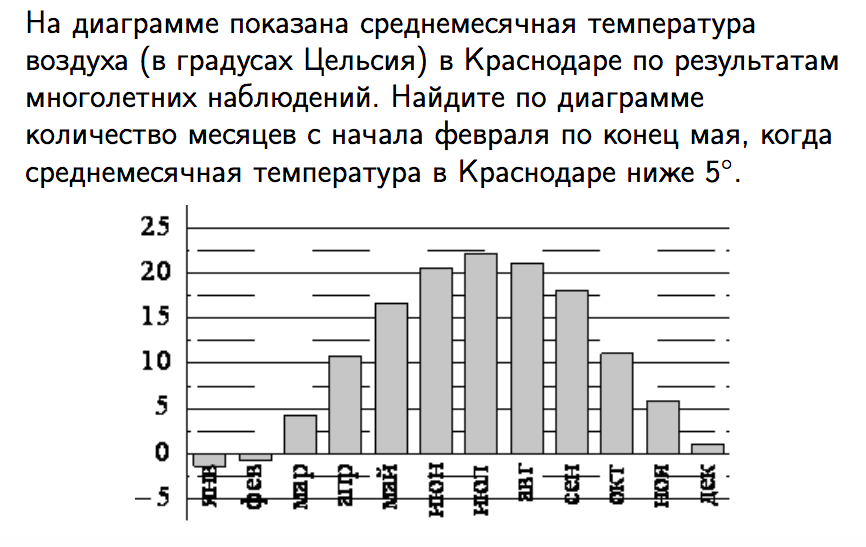
Задание 7: чтение диаграмм

Типичный ответ

Очень часто школьники упускают из виду часть условия «с февраля по конец мая» и дают неправильный ответ на простейшую задачу – «Февраль, март, ноябрь, декабрь».

Хотя правильный ответ

«Февраль и март».

Для решения задачи часто нужно составить уравнение, а для этого важно не упустить ни одного элемента условия и правильно записать его математическим языком. Умение перевести текст задачи в уравнение – навык, который надо тренировать.. Иногда для решения задачи можно и даже нужно использовать элемент, который прямо не прописан в условии.

Иногда для решения задачи можно и даже нужно использовать элемент, который прямо не прописан в условии.

Задание 16: текстовая задача

Вводим неизвестное: х – количество винограда. Чтобы составить уравнение, нам необходимо равенство. Что мы можем в данном случае уравнять? Сухое вещество, ведь оно остается одинаковым и в винограде, и в изюме. Если в винограде 82% воды, значит сухого вещества – 18%. Точно так же находим сухое вещество в изюме: 100 – 19 = 81%.

Получается, что 18% от неизвестного нам количество винограда – это то же самое, что 81% от 42 килограммов изюма. Составляем уравнение и решаем его:

х ∙ 18% = 42 ∙ 81%

Ответ: х = 189.

Задание 3

Составители экзамена проверяют ваш навык работы с процентами. Задачи на проценты бывают трех типов:

Тип 1. Найти часть от числа

Часть
может быть выражена в процентах или сразу в виде дроби. Например, придется
искать треть от чего-то.

Рассмотрим на примере реальной задачи из экзамена:

Прочувствуйте
специфику задачи: нам известно целое — вся зарплата до вычета налога. А
работать мы будем с кусочком — 13-ю процентами. Сколько это в рублях нам еще
предстоит узнать.

Чтобы ответить на вопрос задачи, делаем 3 шага:

А.
Переводим процент в десятичную дробь

Для
этого всегда надо количество процентов поделить на 100.

13 : 100 = 0,13

Б.
Находим, сколько это от зарплаты в рублях

12 500 * 0,13 = 1 625 (р.) —
налог, который удержат с зарплаты Ивана Кузьмича.

В.
Отвечаем на вопрос задачи

У
нас просили зарплату после вычета налога, а не сам налог.

12 500 — 1625 = 10 875 (р.)

Ответ:
10 875.

Будьте внимательны, многие завалятся именно на последнем шаге!

Тип 2. Найти число по его части

Прочувствуйте
разницу с прошлой задачей: тут 124 это и есть 25%, то есть одна и та же
величина выражена в процентах и в абсолютных величинах, в данном случае — в
учениках. Просят узнать целое — 100%.

А.
Переводим процент в десятичную дробь

25 : 100 = 0,25

Б.
Находим, сколько учеников всего

124 : 0,25 = 496 (у.) — всего.

Ответ: 496.

Тип 3. Найти, сколько процентов часть составляет от целого

Особенность
подобных заданий — не дано процентов, есть только абсолютные величины. В данном
случае — стоимость футболки в рублях.

А.
Находим, какую долю новая цена составляет от первоначальной

680 : 800 = 0,85

Б. Переводим долю в процент

В прошлых задачах мы уже дважды выполнили обратное
действие. В этот раз сделаем наоборот: умножим полученную дробь на 100

0,85 * 100 = 85 % — столько процентов
новая цена составляет от старой

В. Отвечаем на вопрос задачи

Нас спросили, на сколько процентов цена снизилась, что
стала 85% от первоначальной? Конечно, изначально она была 100%. Итого

100 — 85 = 15%.

Ответ:
15%

Остался последний тип, не так явно связанный с
процентами…

Тип 4. Задачи на соотношение

Если чуть перефразировать условие, то за первого
кандидата проголосовали 3 части избирателей, а за второго — 2 части.
Особенность этих частей в том, что они ОДИНАКОВЫЕ по величине.

Если одна будет состоять из 10 человек, то за первого
кандидата будет 30, а за второго — 20.

А. Считаем общее количество частей

3 + 2 = 5

Б. Узнаем, сколько голосов составляет одна такая часть

Тут речь о процентах проголосовавших. Сколько всего
проголосовало? Конечно, 100%! Значит каждая из пяти частей «весит»…

100 : 5 = 20%

В.
Отвечаем на вопрос задачи

За
проигравшего проголосовало меньше частей избирателей. В нашем случае 2.

20 * 2 = 40%

Ответ:
40%.

Решение этих задач удобнее всего оформить табличкой

	1 кандидат	2 кандидат	Всего
Части	3	2	5
Абсолютные величины		20% * 2= 40%	100 %

1 часть = 100% : 5 = 20%

Если рассчитываете решать текстовую задачу, включите здравый смысл! Ответ всегда можно проверить на адекватность благодаря обычной логике. Без нее и выстроить ход решения выйдет вряд ли.

Решайте задачи разными способами

Помните о том, что большинство задач можно решить не одним, а несколькими способами. Это поможет вам избежать ошибок, в том числе связанных с выполнением вычислений или обычной невнимательностью.

Если вы решили задачу двумя способами и получили один и тот же ответ, значит, он точно правильный.

При этом выбирайте более простые пути решения, а вот громоздких решений, наоборот, избегайте. Чем проще решение, тем меньше вероятность ошибиться.

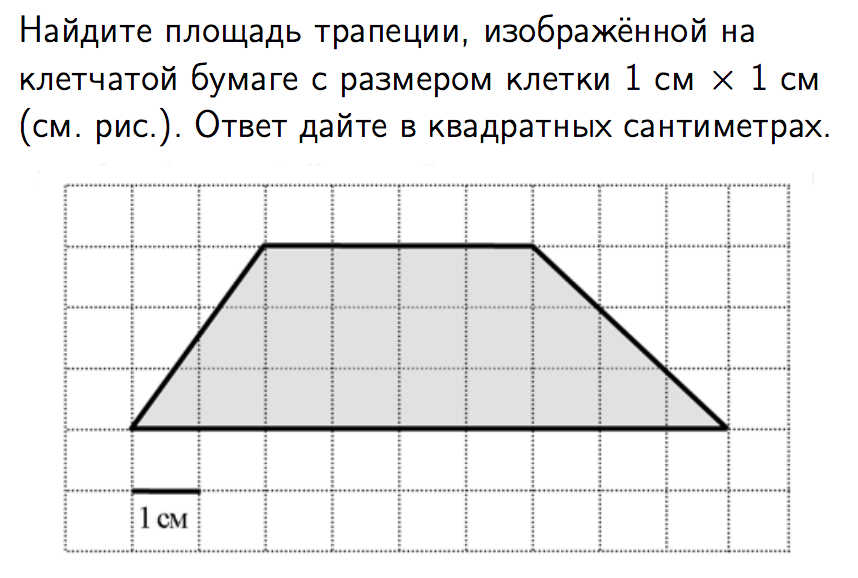
Задание 9: клетчатая бумага

Способ 1. Делим трапецию на два треугольника по краям и прямоугольник в центре. Считаем площадь по клеточкам. Площадь прямоугольника – 12 см2.

Треугольники для удобства продолжаем до прямоугольников, считаем площадь этих прямоугольников (она получается 6 и 9 см2) и делим ее пополам. Таким образом, получается, что площадь первого треугольника – 3 см2, а второго – 4,5 см2. Складываем 3 + 12 + 4,5 и находим площадь трапеции = 19,5 см2.

Способ 2. Используем формулу для нахождения площади трапеции.

S=1/2 ∙h(a+b), где h – высота трапеции, a и b – основания.

S=123(9+4) = 19,5 см2.

Ответ сошёлся, значит он верен.

Не бойтесь математики

Многие задания на экзамене проще, чем кажутся. Правильно считайте, применяйте знание формул, будьте внимательны, и у вас все получится.

Любой нормально развитый человек способен понять математику, и вы — не исключение.

Задача 12: простейший анализ

Чтобы решить эту задачу, нужно знать одну единственную формулу — Ньютона-Лейбница.

S=F(b) – F(а). Подставляем значения х в функцию, указанную в условии, находим F(–1) и F(–3), подставляем в формулу и получаем S=5–3=2.

Задание 15: использование формул

Это одна из самых простых задач с точки зрения математики, хотя и стоит ближе к концу списка заданий. Здесь нужно всего лишь взять формулу, подставить в нее величины и правильно подсчитать.

Обращайте внимание на то, чтобы все упомянутые в задаче числа были указаны в одной системе измерений. При необходимости нужно перевести всё в одну систему, но в данном примере и этого не требуется.. m(t)=31,25

m(t)=31,25

M(0)=250

T=3 мин

Вычисляем и получаем ответ: t=9.

Быстро подготовиться к базовой математике