Школа 2007

Решительные преимущества обучения в ФМШ 2007

Ученики ФМШ 2007 принимают активное участие в турнирах и олимпиадах, начиная с момента основания школы в 2003 году. С тех пор учебное заведение на улице Горчакова выводит своих воспитанников на уровень, дающий им право на льготное зачисление в ведущие вузы. Часть выпускников поступают как призеры олимпиад. Поэтому народный рейтинг физико-математической школы у родителей высок. Как, впрочем, и конкурс на поступление в 5 класс школы 2007. Он составляет обычно не менее пяти претендентов на место.

Победы и призовые места в профильных конкурсах – норма для школы. Дипломов насчитывается в год порядка 1500. Олимпиадное движение – часть учебного процесса. Только в сборной Москвы по информатике состоит 10-12 учащихся из школы № 2007. Кроме трофеев в области физики и математики, копилку пополняют победы в английском языке, биологии и химии.

В программе есть специальный предмет «Практикум по решению задач». Это предмет математического цикла, в котором упор делается не на прохождение конкретных тем, а на развитии общих математических навыков решения задач. Такой подход в корне отличается от натаскивания на шаблонных примерах, как в большинстве учебных заведений.

Особенности и преимущества программы ФМШ в Южном Бутово, доступные для пятиклассников:

  • Практикум по решению задач
  • Участие в олимпиадах
  • Кружки по математике
  • Информатика
  • Естествознание

Качество образования и атмосферу в стенах школы обеспечивает команда преподавателей. Среди них 2 доктора наук, 7 кандидатов наук, 2 заслуженных учителя РФ, 10 почетных работников общего образования, 32 учителя высшей категории и 14 учителей первой категории.

Как проходит поступление в 5 класс школы 2007

Все дети идут по общему конкурсу. Экзамены в ФМШ называют промежуточной аттестацией. Проводятся они обычно с начала апреля до конца мая. Приёмная кампания включает в себя два тура:

  • Письменное собеседование
  • Устное собеседование

На первом этапе ребята пишут контрольную по базовой школьной программе. Отличие от обычной школьной контрольной состоит в более напряженном темпе выполнения заданий. Чтобы ребенок уложился по времени и не ошибся в письменной работе, требуется целенаправленная тренировка. На этом этапе может потребоваться помощь репетитора для поступления в 5 класс школы 2007, который досконально знаком с форматом и особенностями вступительных экзаменов ФМШ.

Второй тур представляет собой устный экзамен, на котором проверяется умение решать нестандартные задачи, без шаблонных алгоритмов. Обычно экзамен состоит из нескольких заданий. При этом требуется решить не менее определённого количества, которое может варьироваться из года в год в зависимости от конкурса. Записывать ответы можно кратко, развернутый ответ дается устно, со всеми требуемыми пояснениями.

Кроме того, в рамках второго тура проводится собеседование, на котором оцениваются:

  • Способность к углубленному изучению математики.
  • Мотивированность на учебу.
  • Уровень эрудиции.

Для сдачи письменного теста предоставляется вторая попытка, для устного – нет. Сумма полученных баллов появляется у каждого школьника в личном кабинете. В плюс идут награды, полученные на Всероссийской олимпиаде школьников и Московской олимпиаде школьников, а также некоторых других математических состязаниях.

Архив записей

Архив записейВыберите месяц Сентябрь 2021  (1) Июль 2021  (1) Июнь 2021  (2) Май 2021  (1) Апрель 2021  (1) Март 2021  (1) Сентябрь 2020  (1) Август 2020  (2) Июль 2020  (2) Июнь 2020  (2) Декабрь 2019  (3) Ноябрь 2019  (4) Октябрь 2019  (3) Сентябрь 2019  (2) Май 2019  (1) Октябрь 2018  (1) Июнь 2018  (1) Апрель 2018  (1) Январь 2018  (1) Ноябрь 2017  (1) Октябрь 2017  (1) Сентябрь 2017  (2) Август 2017  (4) Июль 2017  (5) Июнь 2017  (4) Май 2017  (5) Апрель 2017  (2) Март 2017  (1) Февраль 2017  (1) Январь 2017  (3) Декабрь 2016  (1) Ноябрь 2016  (2) Октябрь 2016  (3) Сентябрь 2016  (4) Август 2016  (6) Июль 2016  (9) Июнь 2016  (4) Май 2016  (5) Апрель 2016  (6) Март 2016  (5) Февраль 2016  (8) Январь 2016  (8) Декабрь 2015  (9) Ноябрь 2015  (4) Июль 2015  (1) Март 2015  (1) Февраль 2015  (1) Январь 2015  (1) Июль 2014  (1) Июль 2013  (1) Март 2013  (2) Декабрь 2012  (1) Ноябрь 2012  (1) Сентябрь 2012  (3) Август 2012  (4) Июль 2012  (4) Июнь 2012  (4) Май 2012  (4) Апрель 2012  (5) Март 2012  (7) Февраль 2012  (8) Январь 2012  (7) Декабрь 2011  (5) Ноябрь 2011  (1)

Экзамен по математике в 5 класс школы 2007

Задание 1. Выполните действия в столбик:
а)
б)
в)

а) :

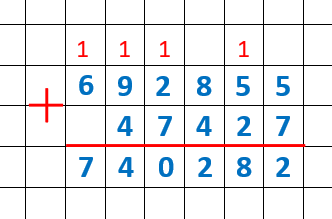
б) :

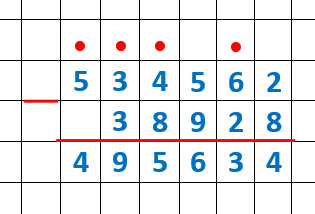
в) :

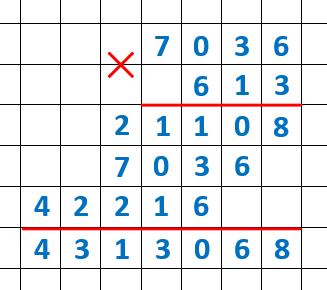
Задание 2. Выполните действия в столбик и поставьте знак больше, меньше или равно так, чтобы получилось верное равенство или неравенство: или

1) .

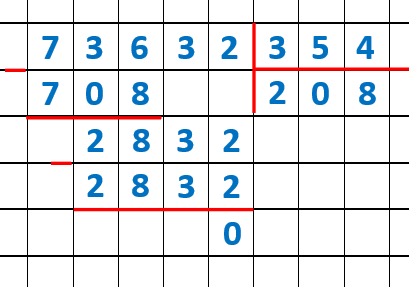
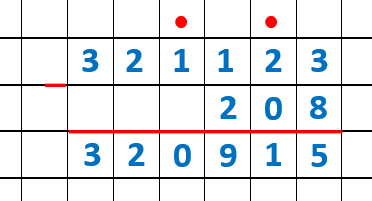
2) .

Ответ: .

Задание 3. Перепишите пример в тетрадь и решите по действиям:

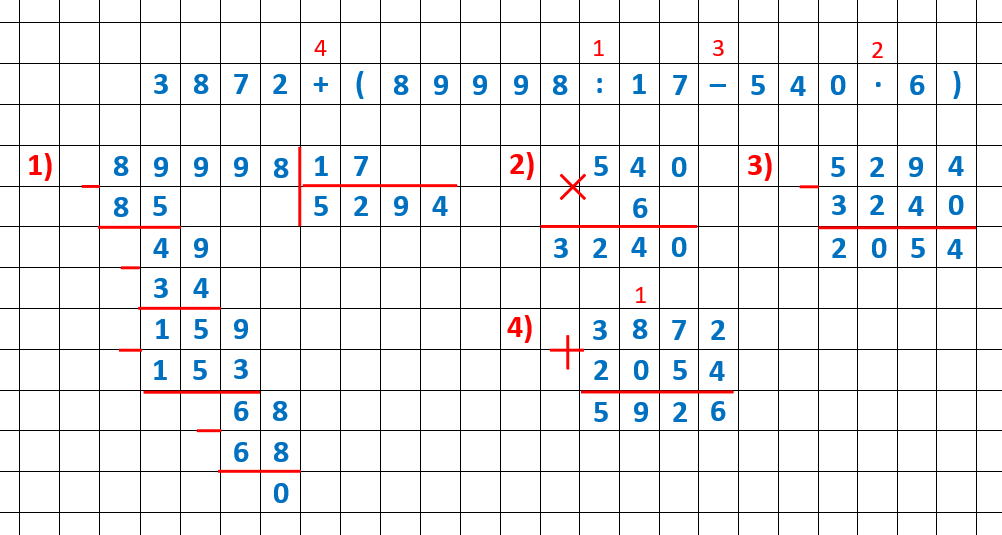
Ответ: .

Задание 4. Всего для украшения парка использовали 780 цветов — ирисы, астры, розы и тюльпаны. Третья часть всех цветов — тюльпаны. Ирисов на 120 меньше, чем тюльпанов. Астр в 3 раза больше, чем роз. Сколько астр в парке?

1) — тюльпанов.

2) — ирисов.

3) — астр и роз вместе.

4) Пусть роз 1 часть. Тогда астр 3 части. Значит, цветов составляют 1 часть.

5) — астр.

Ответ: .

Задание 5. Вычислите, покажите все промежуточные действия:
а) (35 м2 47 см2 — 30 дм2 67 см2) ⋅ 2
б) (18 ч 43 мин 32 с + 1 ч 56 мин 60 с) : 4.

Решение:

а) (35 м2 47 см2 — 30 дм2 67 см2) ⋅ 2

Используем, что:

  • 1 м2 = 100 см ⋅ 100 см = 10 000 см2
  • 1 дм2 = 10 см ⋅ 10 см = 100 см2

Тогда получаем следующее:

  • 35 м2 47 см2 = 350 000 см2 + 47 см2 = 350047 см2.
  • 30 дм2 67 см2 = 3000 см2 + 67 см2 = 3067 см2.
  • 350047 см2 — 3067 см2 = 346 980 см2
  • 346 980 см2 ⋅ 2 = 693 960 см2 = 69 м2 39 дм2 60 см2

б) (18 ч 43 мин 32 с + 1 ч 56 мин 60 с) : 4

Теперь используем, что:

  • 1 мин = 60 с
  • 1 ч = 60 мин = 60 ⋅ 60 с = 3600 с

Тогда получаем следующее:

  • 18 ч + 1 ч = 19 ч
  • 43 мин + 56 мин = 99 мин = 1 ч 39 мин
  • 32 с + 60 с = 92 с = 1 мин 32 с
  • 19 ч + 1 ч 39 мин + 1 мин 32 с = 20 ч 40 мин 32 с
  • (20 ч 40 мин 32 с) : 4 = 5 ч 10 мин 8 с

Ответ: а) 69 м2 39 дм2 60 см2 б) 5 ч 10 мин 8 с

Задание 6. Братья Даня и Ваня вышли из дома одновременно в противоположных направлениях. Даня пошёл пешком со скоростью 42 м/мин к бабушке, а Ваня поехал на велосипеде в школу со скоростью 158 м/мин. Расстояние от дома мальчиков до дома бабушки — 756 метров. Даня всю дорогу шёл без приключений. У Вани через 12 минут после старта сломался велосипед, он остановился и 3 минуты пытался его починить. Поскольку починить велосипед не получилось, дальше Ваня шёл до школы пешком. Братья добрались до своих целей одновременно.
а) Сколько времени Ваня шёл пешком?
б) На каком расстоянии друг от друга были мальчики, когда Ваня начал идти пешком?

1) мин — время движения Дани. Столько же в общей сложности по времени двигался и Ваня.

2) мин — Ваня шёл пешком.

3) м — проехал Ваня на велосипеде до остановки.

4) м — прошёл Даня до момента, когда начал идти Ваня.

5) м — расстояние между мальчиками, когда Ваня начал идти пешком.

Ответ: а) мин; б) м.

Задание 7. Маша задумала число и увеличила его в 3 раза. Вычла результат из числа 80. Полученное число уменьшила в 2 раза. Поменяла местами цифры в числе. Увеличила результат на самое большое однозначное число и получила 40. Какое число задумала Маша?

Идём в обратной последовательности:

5) Наибольшее однозначное число — это . Значит, перед последним действием у Маши было число .

4) Маша получила число , переставив цифры некоторого числа местами. Значит, до этого у неё было число .

3) Тогда число было на шаг раньше.

2) До этого у Маши было число .

1) Значит, исходное число, которое загадала Маша, было равно .

Ответ: .

Задание 8. Старик Хоттабыч и Волька едят мороженое с постоянной скоростью. За 60 минут Хоттабыч съедает 6 эскимо, а Волька — 10 эскимо. Они начали есть одновременно, и съели одинаковое количество мороженого, но Хоттабыч ел на 20 минут дольше Вольки. Сколько эскимо съел Хоттабыч?

1) минут тратит Волька на поедание 1 мороженого.

2) минут тратит Хоттабыч на поедание 1 мороженого.

3) На минуты Хоттабыч тратит больше, чем Волька на поедание 1 мороженого.

4) Так как всего Хоттабыч потратил на 20 минут больше, чем Волька, чтобы съесть такое же количество мороженых, то мороженых съел Хоттабыч.

Ответ: .

Задание 9. Мама испекла прямоугольный пирог с разными начинками: вишней, малиной, клубникой и шоколадом (см. рисунок):

Каждая шоколадная часть квадратной формы со стороной 7 см. Общая площадь малиновых частей в три раза больше, чем общая площадь клубничных частей. Зная, что ширина пирога 26 см, найдите:
а) периметр вишнёвой части пирога;
б) общую площадь пирога.

Подробное решение задания представлено в этом видео:

https://youtube.com/watch?v=ALqjy72Wsxg

Конспект решения:

1) см — длина клубничной части.

2) см — длина малиной части.

3) см — периметр вишнёвой части.

4) см — длина пирога.

5) см2 — площадь пирога.

Ответ: а) см; б) см2.

Если вам требуется подготовка к поступлению в школу 2007, то обращайтесь ко мне. Я являюсь профессиональным репетитором и имею обширный успешный опыт такого рода подготовки. Чем раньше начать подготовку, тем лучше. Можно даже летом. Мои контакты вы найдёте на этой странице.

Похожие записи:

Кто такой лингвист и сколько на него учится? Кафедра товароведения и технологии общественного питания Профессия event-менеджер Default ThumbnailСписки поступающих в железнодорожный колледж в ростове [уроки автокад] полный видеокурс автокад с нуля бесплатно «двухмерное проектирование» Default ThumbnailАрхитектурно-строительные вузы россии